12. Heaps

Feel free to use your laptop
You are strongly encourage to work with others
- When you get stuck, ask those sitting around you for help
- Get used to working together in the labs
- Peer teaching and peer learning has been empirically shown to be very effective

Note

This topic has not been covered in lectures, but at this stage, this should not be a problem.

12.1. Heaps

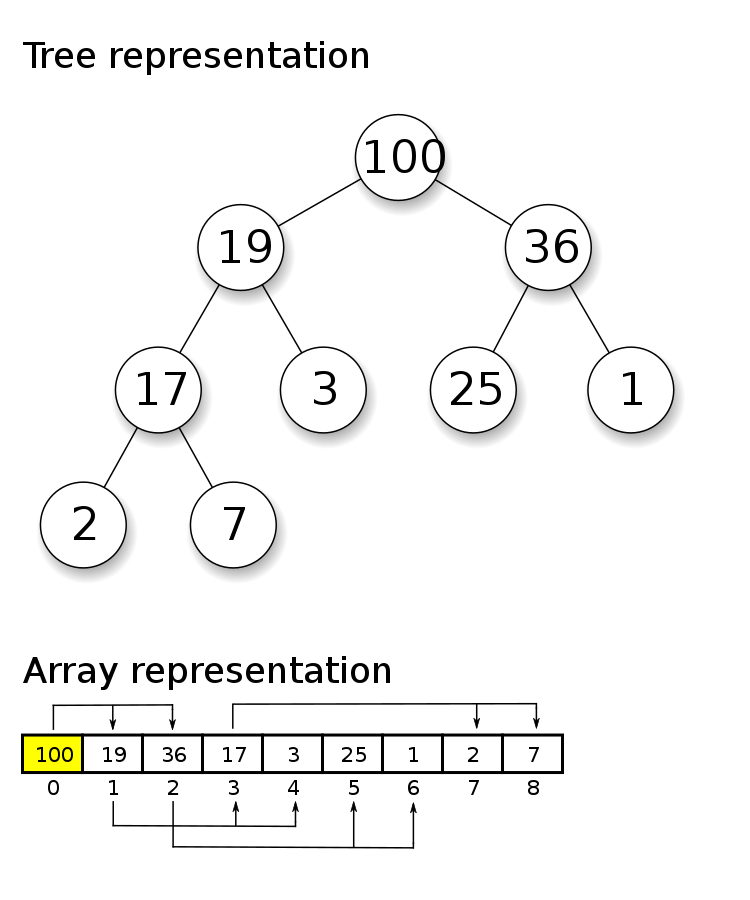
../../_images/heap_example.png — A heap is encoded within an array but represents a binary tree structure. This particular heap is an example of a “max heap”, which is a heap where each node contains values larger than those of their children.

The root of the tree is always at index \(0\)
Given an element at index \(i\)
- Its left child can be found at \(2i + 1\)
- Its right child can be found at \(2i + 2\)
- Assuming it’s not the root, it’s parent can be found at \(\lfloor (i-1)/2 \rfloor\)
  \(\lfloor x \rfloor\) just means to round down if needed
For example, consider the element 17 located at index \(3\) in the array
- Left child would be at \(3*2 + 1 = 7\)
- Right child would be at \(3*2 + 2 = 8\)
- Parent would be at \(\lfloor (3-1)/2 \rfloor = 1\)

12.2. Min Heap

A min heap is a special heap with the property that the parent must be smaller than their children
- Or, children of an element must be greater than their parent
In other words, the root must be the smallest element in the tree
- This definition can be recursively applied to all subtrees within a tree
A max heap is similar to a min heap, but instead the root is the largest
- The image above provides an example of a max heap

Warning

Although min/max heaps are binary trees, they are not binary search trees; do not get the idea of min/max heaps confused with binary search trees. Where binary search trees have the ordering based on left/right orientation, the min/max heaps have their ordering based on up/down direction.

12.2.1. Bubble Up

Whenever something is added to the heap, it is placed at the next available index in the array
- This ensures that our heap is always a complete binary tree
However, if the goal is to make a min heap, simply adding something to the end may cause a problem since it may have a value less than its parent
Fortunately, there is a simple way to address this issue — Bubbling up
If the value at the index \(i\) is less than the value at the index of \(\lfloor (i-1)/2 \rfloor\) — its parent
- Swap the values
Repeat this process for the inserted value until either
- The inserted value is not less than the parent’s value
- The inserted value is at the root

12.2.2. Bubble Down

Given the min heap’s property of the smallest element being at the root, it is often used for keeping track of ordered data
- The minimum value in a collection is always at index \(0\)
Unfortunately, if the minimum value is to be removed, there will be no value at the root of the tree
- A solution to this problem is to bubble down
Remove the element at the last index in the heap and place it in the root position \(i = 0\)
Compare the moved value with its left and right children at indices \(2i + 1\) and \(2i + 2\)
- Swap the value with the smaller of the two children’s value
Repeat this process until either
- The value is not greater than either child
- There are no more children to compare to; the value is at a leaf

12.3. Implement a Min Heap

Create a generic ArrayMinHeap class
- public class ArrayMinHeap<T extends Comparable<? super T>>
Include fields to keep track of the size and the array containing the elements
Implement the following methods
- add
- size
- remove
- peek
Consider adding the following private methods
- bubbleUp
- bubbleDown
- expandCapacity
- parentOf
- leftChildOf
- rightChildOf
- swap
Test the heap to see if it is working properly
- Simply create an instance of the MinHeap and use the implemented methods to check correctness
- For the purpose of the lab, do not worry about writing full unit tests