12. Algorithm Analysis

• What does it mean for an algorithm to be good?

• What makes one algorithm for solving a given problem better than another?

• Does the algorithm have a practical runtime?

• These questions can be answered in many ways, but one important measurement is how much resources does your algorithm need?

  • How much time to compute?

  • How much memory does it need?

  • How many processors does it need?

  • How does the amount of resources change relative to some input value?

• The above considerations are all important, but here, the focus is on Time Complexity

12.1. Time Complexity

• The amount of time an algorithm needs relative to the input size

  • How long does it take to sort 10 items?

  • How long does it take to sort 10,000 items?

• Considers the number of operations needed for the algorithm, and the time complexity of those operations

  • Addition

  • Comparisons

• With an understanding of an algorithm’s time complexity, one can make informed decisions when picking the tools for a job

  • For example, which data structures to use in certain scenarios

12.2. Growth Function

• It is important to understand the relationship between the size of the input \(n\) and the time it takes to run an algorithm \(t(n)\)

  • For example, the size of input could be the length of a list to be sorted

  • How does the time to run the algorithm \(t(n)\) change as \(n\) changes?

• This \(t(n)\) is called the growth function

• Notice how \(t(n)\) is a function of \(n\)

  • This means the amount of time depends on \(n\)

• Consider this arbitrary growth function — \(t(n) = 15n^{2} + 45n\)

  • Details on deriving the growth function is discussed below

How the growth function and the individual parts of the growth function change as \(n\) increases.

\(n\)	\(15n^{2}\)	\(45n\)	\(15n^{2} + 45n\)	\(\frac{15n^{2}}{15n^{2} + 45n}\)
1	15	45	60	0.25
2	60	90	150	0.40
5	375	225	600	0.625
10	1,500	450	1,950	0.769230769
100	150,000	4,500	154,500	0.970873786
1,000	15,000,000	450,000	15,045,000	0.997008973
10,000	1,500,000,000	450,000	1,500,450,000	0.99970009
100,000	150,000,000,000	4,500,000	150,004,500,000	0.999970001
1,000,000	15,000,000,000,000	45,000,000	15,000,045,000,000	0.999997

• This table shows how each of the parts of the \(t(n)\) growth function changes as \(n\) grows

• Take note as to which part can be blamed for most of the total work done within \(t(n)\)

• When \(n\) is small, which part of the expression gives a larger value?

• As \(n\) grows, which becomes bigger?

• How much do the constants (\(15\) and \(45\)) impact the values?

  • Do they affect how big the numbers change as \(n\) increases?

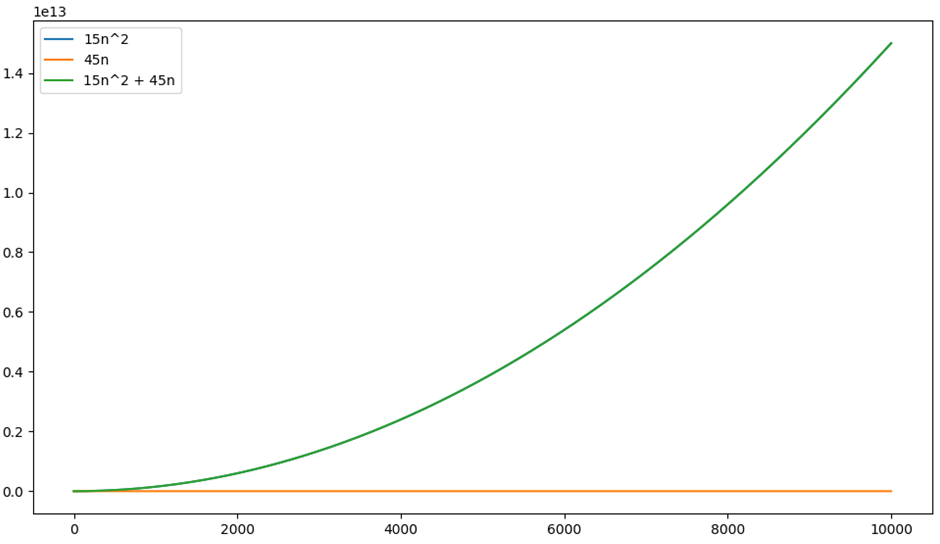
Plot of \(t(n)\) (y-axis) against \(n\) (x-axis). Note that \(15n^{2}\) is covered by \(15n^{2} + 45n\) as their growths are so similar at this scale. Further, at this scale, the portion of the the growth function that is linear (\(45n\)) appears to be a horizontal line.

• This figure compares the individual parts of the growth function to the growth function itself

• Notice the scale of the axes

• Also notice how the blue \(15n^{2}\) line is perfectly covered by the green \(15n^{2} + 45n\) line

• See how the part that grows linearly, \(45n\), appears to be a horizontal line at this scale

  • In other words, the \(45n\) part of the function is effectively inconsequential in this context

• Given this, and the fact that constants only scale the values, we say that the \(n^{2}\) is the dominant term

Warning

One thing students tend to miss when first learning about computational complexity is that the function describes how things change relative to \(n\). At this stage, the discussion is not about any absolute runtime value.

For example, given this growth function \(t(n) = n^{2} + 999n\) one may say that the \(999n\) part of the function is going to dominate for all values \(n < 999\), which is true. However, this is not the point of complexity analysis. The point is identifying which part of the function grows faster, and in this example, \(n^{2}\) grows faster.

This is not to suggest that the observation of when \(n < 999\) is not important or valuable; this is only to highlight that the focus here is about change and growth.

12.3. Asymptotic Growth & Big-O

• Constants and coefficients are not too important

• Non dominant terms are not too important

• The actual growth function is not that important

• The asymptotic complexity is important

  • The time the algorithm takes, as a function of \(n\), will grow like…

• The order of the algorithm is specified using Big-O notation

• The above example, \(t(n) = 15n^{2} + 45n\), has an order of \(O(n^{2})\) since it grows like \(n^{2}\)

12.3.1. Example Growth Functions and Their Order

Example growth functions with their order denoted in Big-O notation.

Growth Function	Order
\(t(n) = 17\)	\(O(1)\)
\(t(n) = 20n - 4\)	\(O(n)\)
\(t(n) = 12n \log_{2}(n) + 100n\)	\(O(n\log_{2}(n))\)
\(t(n) = 3n^{2} + 5n - 2\)	\(O(n^{2})\)
\(t(n) = 2^{n} + 3n\)	\(O(2^{n})\)

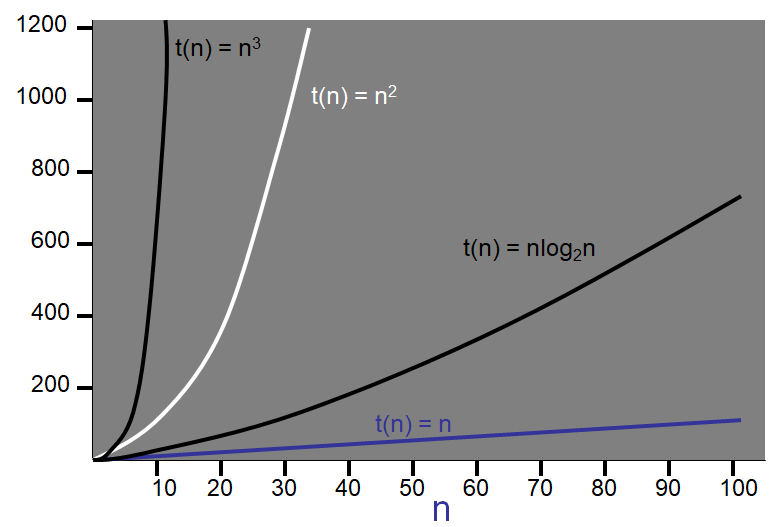
Example curves of common time complexities.

• It is typical to see the order of a growth functions expressed as one of a few common expressions

Example growth functions with their order left blank as an exercise.

Growth Function	Order
\(t(n) = 5n^{2} + 3n\)	\(O(?)\)
\(t(n) = n^{3} + \log_{2}(n) - 4\)	\(O(?)\)
\(t(n) = 10n \log_{2}(n) + 5\)	\(O(?)\)
\(t(n) = 3n^{3} + 3n^{2} + 3\)	\(O(?)\)
\(t(n) = 2^{n} + 18n^{10}\)	\(O(?)\)

12.4. Deriving Growth Functions

• Growth functions, \(t(n)\), are derived by investigating the code

Note

For simplicity, constant time (\(O(1)\)) statements will be said to take \(1\) unit of work. In reality, they may take more, but they will ultimately still take constant time, and constants are ignored.

12.4.1. Statements

int x = 0;      // 1 unit of work
int y = 1;      // 1 unit of work
int z = x + y;  // 1 unit of work

Growth Function: \(t(n) = 3\)

Order: \(O(1)\)

12.4.2. Loops

• The number of times a loop executes may dependant on some value \(n\)

int x = 0;                      // 1 unit of work
for (int i = 0; i < n; i++) {
    x = x + 1;                  // 1 unit of work n times (1*n)
}

Growth Function: \(t(n) = 1 + 1n\)

Order: \(O(n)\)

• With a loop, consider a number line

• The \(i^{th}\) number in the number line is visited each time the loop executes a single iteration

• How many numbers were visited?

Example number line of length \(n\).

12.4.3. Nested Loops

• This can feel tricky, but there is no trick beyond the rules discussed so far

int x = 0;                          // 1 unit of work
int y = 0;                          // 1 unit of work
for (int i = 0; i < n; i++) {       // Everything in loop runs n times
    x = x + 1;                      // 1 unit of work n times (1*n)
    for (int j = 0; j < n; j++) {   // Runs n times and everything in this loop runs another n times
        y = y - 1;                  // 1 unit of work n times, n times
    }
}

• It may be easier to work from the inside out

Growth Function: \(t(n) = (1n + 1)n + 2 = n^{2} + n + 2\)

Order: \(O(n^{2})\)

• Consider the below \(n \times n\) matrix in the context of the above code

  • y = y - 1; is represented by a single spot in the matrix (constant time operation)

  • y = y - 1; runs \(n\) times by a loop, which is represented by a single row

  • The whole loop that contains y = y - 1 is within another loop that is run \(n\) times, which is represented by all rows

  • How many things were visited?

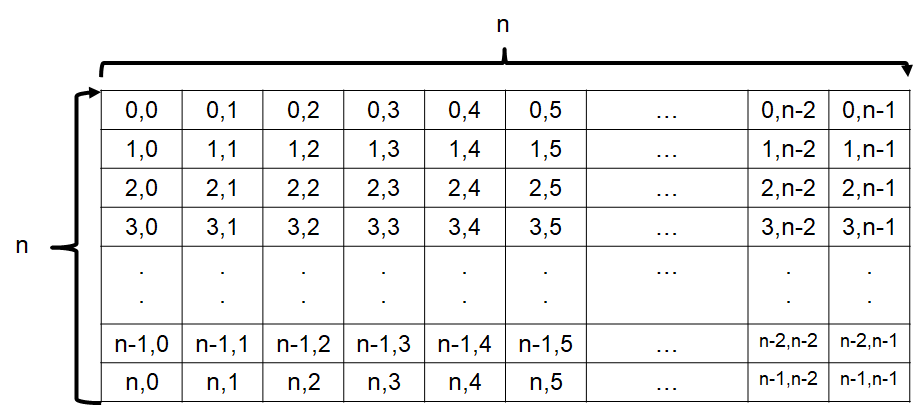
Example \(n \times n\) matrix.

12.4.4. Exercises

int x = 0;
for (int i = 0; i < n; i = i + 2) {     // note how i is incremented
    x = x + 1;
}

• HINT: Keep the number line of length \(n\) in mind

Growth Function: \(t(n) = ?\)

Order: \(O(?)\)

int x = 0;
int y = 0;
for (int i = 0; i < n; i++) {
    x = x + 1;
    for (int j = i; j < n; j++) {       // j starts at i
        y = y - 1;
    }
}

• HINT: Keep the \(n \times n\) matrix in mind

Growth Function: \(t(n) = ?\)

Order: \(O(?)\)

int x = 0;
for (int i = 1; i < n; i = i * 2) {     // note how i is updated
    x = x + 1;
}

• HINT: Keep the number line of length \(n\) in mind

• HINT: How quickly will the numbers in the number line run out?

Growth Function: \(t(n) = ?\)

Order: \(O(?)\)

12.5. Stack Comparisons

• Two implementations of the stack were implemented

• Stacks are pretty efficient in general, but which is better?

  • LinkedStack vs ArrayStack

12.5.1. Popping & Peeking

    @Override
    public T pop() {
        if (isEmpty()) {
            throw new NoSuchElementException("Empty stack");
        }
        T returnElement = top.getData();
        top = top.getNext();
        size--;
        return returnElement;
    }

    @Override
    public T peek() {
        if (isEmpty()) {
            throw new NoSuchElementException("Empty stack");
        }
        return top.getData();
    }

    @Override
    public T pop() {
        if (isEmpty()) {
            throw new NoSuchElementException("Empty stack");
        }
        T returnElement = stack[top - 1];
        stack[top - 1] = null;
        top--;
        return returnElement;
    }

    @Override
    public T peek() {
        if (isEmpty()) {
            throw new NoSuchElementException("Empty stack");
        }
        return stack[top - 1];
    }

12.5.2. Pushing

    @Override
    public boolean push(T element) {
        Node<T> toPush = new Node<T>(element);
        toPush.setNext(top);
        top = toPush;
        size++;
        return true;
    }

    @Override
    public boolean push(T element) {
        if (size() == stack.length) {
            stack = expandCapacity(stack);
        }
        stack[top] = element;
        top++;
        return true;
    }

    /**
     * Returns a new array with double the size of the stack array container and copy the contents from the old array to
     * the new array.
     */
    @SuppressWarnings("unchecked")
    private T[] expandCapacity(T[] oldStack) {
        T[] newStack = (T[]) new Object[oldStack.length * 2];
        for (int i = 0; i < oldStack.length; i++) {
            newStack[i] = oldStack[i];
        }
        return newStack;
    }

12.6. For Next Time

• Read the amortized time complexity aside

• Read Chapter 2 of your text

  • 14 pages