28. Sorting
Like searching, sorting is a classic problem
Everyone has sorted things before
The problem is well understood
But how much time has been spent really analyzing the process of sorting?
Perhaps even more interesting, until relatively recently, humans have been pretty terrible at it
There are many sorting algorithms out there
They will work different ways, but result in sorted collections
Some will more or less be the same in terms of the amount of computation required
And some will be much better than others
Note
Most of the sorting images are taken directly from their wikipedia articles. Click the image to visit their respective pages.
28.1. Sorting Problem
Given a collection of things
Numbers
Strings
People
Car Parts
The goal is to arrange the collection of things such that they are in order
28.1.1. Order
What in order means however will depend on what is being sorted
For example
Numbers come with an intrinsic ordering
Java uses the Natural Order
“This ordering is referred to as the class’s natural ordering, and the class’s compareTo method is referred to as its natural comparison method.”
Strings could be ordered alphabetically
Perhaps by length?
Sort people based on height
Or age?
Or month and day of birthday?
Car Parts by mass?
Or production code?
Date they were made?
Volume?
The amount of dust particles on the surface?
With numbers, there’s no need to ask
But with other things, a well defined ordering is needed for the things
The things themselves have the order-ness property, not a sorting algorithm
The orderness has already been discussed a few times in the context of an ordered bag and binary search tree
More complex orderings can also be defined
For example, comparing things based on multiple values
For example, sorting music by artist and year
Note
For ease, numbers are used in the examples, but the ideas are generalizable to other things if they have a defined order.
Here, a collection of numbers is considered ordered if and only if the elements are monotonically increasing. This is just fancy way of saying the numbers are always increasing or are equal, but never decreasing. For example:
\(1, 2, 3, 5, 5, 6, 8, 8, 8, 9\)
28.2. Bogosort
Here’s a fun idea
Given a function called
isSorted(collection)that returns true if the collection is sorted and false otherwise\(O(n)\)
And given another function called
shuffle(collection)that randomly shuffles the collection\(O(n)\)
Think of shuffling a deck of cards
The algorithm is then:
while not isSorted(collection): shuffle(collection)
Best case scenario, get luck with the collection already being sorted —
isSortedis called only onceWorst case is… forever?
It’s possible to get really unlucky and shuffle the elements such that they are the same not in order order every time
This is obviously not a particularly great sorting algorithm in terms of the computation required
If \(n\) is very small, there’s a reasonable chance to end up with a sorted collection after a while
But to put things into perspective, there are a total \(8.0658175 \times 10^{67}\) permutations of a deck of 52 cards
!To put this in perspective, there are roughly \(2.4 \times 10^{67}\) atoms in the Milky Way
If assigning orderings to individual atoms in the Milky way, there would be roughly \(5.7\times10^{67}\) orderings left over
28.3. Bubble Sort
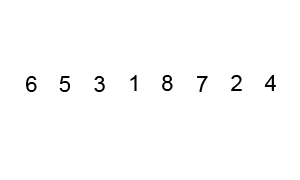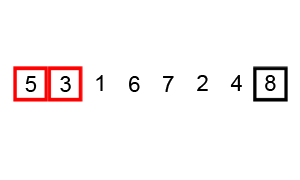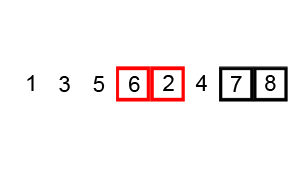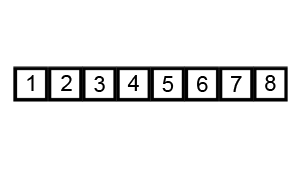
Animation of Bubble Sort.
The general idea of bubble sort is to look at the list, and if any adjacent numbers out of order, swap them
What’s neat about this is the order the swaps are applied does not matter
\(4, 3, 2, 1\)
With the above example, one possible route could be
\(4, 3, 2, 1\)
\(3, 4, 2, 1\)
\(3, 2, 4, 1\)
\(2, 3, 4, 1\)
\(2, 3, 1, 4\)
\(2, 1, 3, 4\)
\(1, 2, 3, 4\)
And another route is
\(4, 3, 2, 1\)
\(4, 3, 1, 2\)
\(3, 4, 1, 2\)
\(3, 1, 4, 2\)
\(3, 1, 2, 4\)
\(1, 3, 2, 4\)
\(1, 2, 3, 4\)
Selecting an arbitrary pair of values to switch works, but a more systematic strategy would be better
Instead of randomly selecting pairs, start at the beginning and look at each adjacent pair and move up the list
Pass 1
\(4, 3, 2, 1\)
\(3, 4, 2, 1\)
\(3, 2, 4, 1\)
\(3, 2, 1, 4\)
However, simply doing one pass does not guarantee that the list will be in order
In fact, all it does guarantee is that the largest value in the list will have bubbled up to its correct spot
The trick is to repeat this process until the list is sorted
Pass 2
\(3, 2, 1, 4\)
\(2, 3, 1, 4\)
\(2, 1, 3, 4\)
Pass 3
\(2, 1, 3, 4\)
\(1, 2, 3, 4\)
28.3.1. Worst Case Scenario
The above example showed the worst case scenario for this specific bubble sort idea
This case here is where the list is in reverse order
But the true worst case scenario is when the smallest element is at the wrong end
The question is, how many passes must be done to guarantee that the list is sorted?
If the list is length \(n\)
And after a single pass the largest value is in its proper location
After a second pass, the second largest value is in its proper location
After a third, the third largest will be where it needs to
…
After \(n\) passes, list is sorted
Actually, \(n-1\) since putting the \((n-1)^{th}\) thing in its proper spot would result in also having the last element, the \(n^{th}\), also in its proper spot
See the above example, where \(n = 4\) and only needing 3 passes
28.3.2. Best Case Scenario
Consider the case where the list is already in order
\(1, 2, 3, 4\)
It may feel rather silly doing a total of \(n-1\) passes since after a single pass it can be concluded that it’s already sorted
In this case, an easy way to stop the sort early is to check if a pass is ever completed with no swaps
If nothing was swapped, then nothing was out of order, therefore the list must be sorted
28.3.3. Algorithm
1While the list is not sorted
2 For each adjacent pair of values
3 If they are out of order
4 Swap them
5 Note that the list is not yet known to be sorted
28.3.4. Computational Complexity
For the best case scenario, a complete pass over all \(n\) elements is needed
This is because it can only be conclude that the collection is sorted by looking at the whole list
Best case \(O(n)\)
For the worst case, each pass is \(O(n)\), but a total of \(n-1\) passes are needed
Worse Case \(O(n^{2})\)
28.4. Insertion Sort
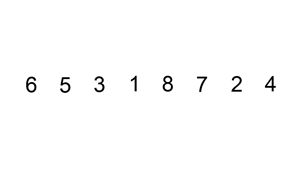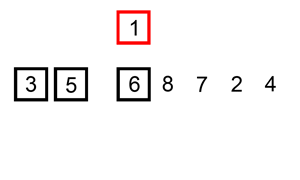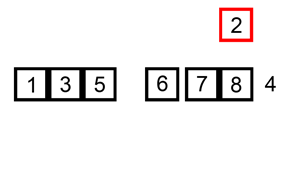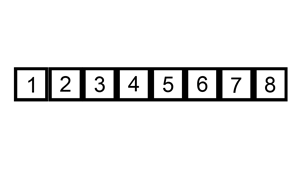
Animation of Insertion Sort.
The idea of insertion sort is to select elements from the unsorted list and insert them into a sorted list in the correct spot such that the sorted list remains sorted
In the above animation, there is a single list with a sorted and unsorted part
Similar to bubble sort, the order that elements from the unsorted list are selected in does not matter in terms of getting a sorted collection in the end
Unsorted |
Sorted |
|---|---|
\(4, 3, 2, 1\) |
|
\(3, 2, 1\) |
\(4\) |
\(3, 2\) |
\(1, 4\) |
\(3\) |
\(1, 2, 4\) |
\(1, 2, 3, 4\) |
Typically, for ease, each element in the unsorted list is picked for insertion in the order that they appear
28.4.1. Computational Complexity
To think of the computational complexity, consider a list of size \(n\)
For each element selected, the location in the sorted list where it must be inserted needs to be found
If this is the first element being selected, then there is nothing in that sorted list, therefore finding where the element should be inserted is trivial
If it’s the second element, one element in the sorted list must be looked at to determine where the second element goes
If it’s the third element, two elements in the sorted list must be looked at
…
If considering the \(n^{th}\) element from the unsorted list, \(n-1\) elements in the sorted list must be looked at
If sorting \(n\) things
All \(n\) things need to be inserted into the sorted list
And \(\frac{n}{2}\) things are looked at on average to find the insertion spot
Therefore, it’s \(O(n^{2})\)
28.4.2. Worst Case Scenario
The situation for the worst case scenario would be if, for each of the \(n\) elements to be sorted, it had to be compared to every single element in the sorted part
For example, in the above animation, the worst case scenario would be if the numbers were in reverse order
Put the largest element (8) in the sorted list
Then take the next largest (7), and put it on the other side of the largest (8)
Then take the third largest (6), and it has to go on the other side of all elements already sorted (7, 8)
…
Take the last element, which happens to be the smallest (1), and go over the whole sorted list to find where it belongs (2, 3, 4, 5, 6, 7, 8)
However, if the list was scanned starting at index 0 each time, the worst case scenario configuration would be if the elements were already in order
28.4.3. Best Case Scenario
The situation for the best case would be if, for each of the \(n\) elements, only compare it to one thing
In the animation example, the best case would be if the list happened to already sorted
Put the smallest element (1) in sorted
Select the next smallest (2), and since it’s larger than the smallest (1), there is no need to look past it
Select the next one (3), and since it’s larger than the second smallest (2), there is no need to look past it
…
Look at the last element, the largest (8), and compare it to the sorted list and see that it is larger than the first thing it considers (7), therefore there is no need to look past it
Like the worst case scenario, the best case scenario configuration depends on which way the elements in the sorted list are looked at
28.4.4. Algorithm
1For each element in the unsorted list
2 Scan the sorted list to find where the new element goes
3 Insert the new element into the sorted list
28.5. Selection Sort
Animation of Selection Sort.
The general idea is
Scan the collection for the smallest element and put it in a sorted list
Scan the collection for the next smallest element and add it to the end of the sorted list
Scan the collection for the next smallest element and add it to the end of the sorted list
…
Unsorted |
Sorted |
|---|---|
\(4, 3, 2, 1\) |
|
\(4, 3, 2\) |
\(1\) |
\(4, 3\) |
\(1, 2\) |
\(4\) |
\(1, 2, 3\) |
\(1, 2, 3, 4\) |
28.5.1. Algorithm
In fact, the basic idea is more or less the algorithm
1For each element in the unsorted list
2 Scan the unsorted list for the next smallest element
3 Add element to the end of the sorted list
28.5.2. Computational Complexity
Assuming a collection of \(n\) elements that need to be sorted
For each element, do a linear search through the unsorted collection for the current smallest element
\(O(n)\)
First time, look at \(n\) elements
Next time, look at \(n-1\) elements
Then \(n-2\) elements
…
Given \(n\) things that need to be sorted
Each pass of the collection puts one element in its place, thus \(n\) passes are needed
Each pass requires a linear search, which takes \(O(n)\)
Therefore, it’s \(O(n^{2})\)
28.5.3. Best and Worse Case Scenario
An interesting thing about selection sort is that there is no difference between the best or worse case scenarios
No matter the configuration of the unsorted collection, an \(O(n)\) linear search must be done for each of the \(n\) elements to be sorted
So, where insertion and bubble had a best case of \(O(n)\) and worse case of \(O(n^{2})\), selection sort is always going to be \(O(n^{2})\)
28.6. For Next Time
Read Chapter 9 Section 2
26 pages