15. ArrayQueue

• Things needed for the implementation

  • A container

  • A way to keep track of the front/head

  • A way to keep track of the rear/tail

  • A way to keep track of the size

• A linked structure was used as a container for a Queue

• Now an array will be used to implement the Queue

15.1. Idea #1

• Use an array for the container

• Keep track of the front by simply having it always be index 0

• Keep track of the rear index

• Size will conveniently be equal to rear

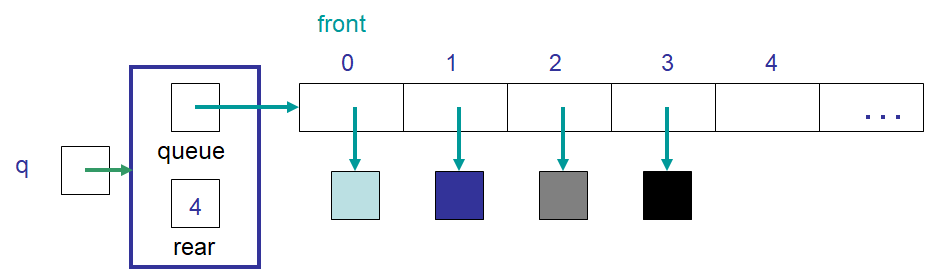
An example of idea #1’s ArrayQueue containing four elements. This implementation requires that index 0 always be the front. Note the value stored in rear refers to the next available spot in the array. Also notice that the value in rear corresponds to the number of elements currently in the queue.

• All adding (enqueue) happens at the rear end

• Add the element to index rear

• Increment rear

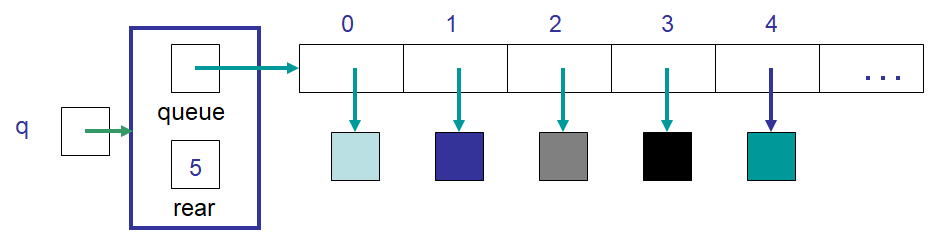
The state of idea #1’s ArrayQueue after an element was enqueued. Note that the element was added at index rear and the value of rear was increased such that it refers to the next available spot in the array.

• All removing (dequeue) happens at index 0

• Requires that elements are shuffled down 1 index

• Decrement rear

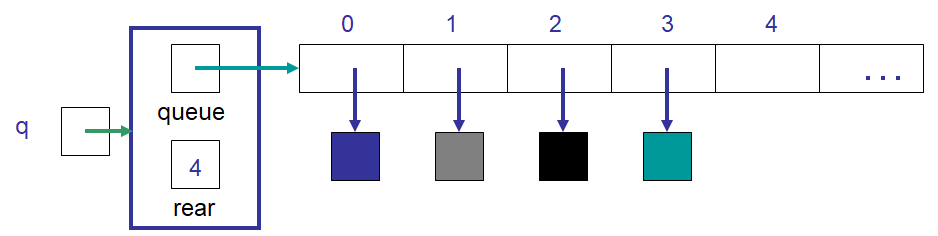
The state of idea #1’s ArrayQueue after an element was dequeued. Note that the element at index 0 was removed and all elements moved down one index in the array. Further, the value of rear was decreased by one.

15.1.1. Discussion

• Will this implementation work?

  • Is it correct?

• Knowing that this is an array implementation, will something like an expandCapacity be required?

• What is the computational complexity of an enqueue with this idea?

  • Amortized \(O(1)\)

• What is the computational complexity of a dequeue with this idea?

  • \(O(n)\) as it requires all \(n\) elements be shuffle down one index in the array

• The drawback of idea #1 is a \(O(n)\) dequeue

  • The LinkedQueue implementation has an \(O(1)\) dequeue

15.2. Idea #2

• Use an array for the container

• Keep track of the front index

• Keep track of the rear index

• Size will conveniently be rear - front

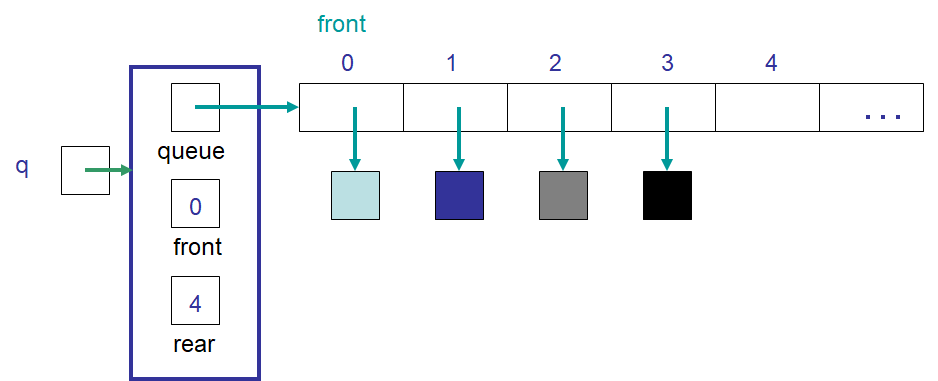
An example of idea #2’s ArrayQueue containing four elements. This implementation keeps track of the front and rear indices. Note the value stored in rear refers to the next available spot in the array. Also notice that the difference between rear and front corresponds to the number of elements currently in the queue.

• All adding (enqueue) happens at the rear end

• Add the element to index rear

• Increment rear

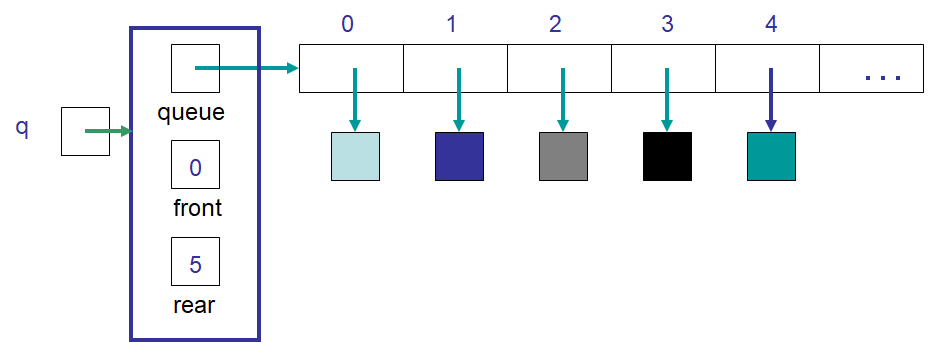
The state of idea #1’s ArrayQueue after an element was enqueued. Note that the element was added at index rear and the value of rear was increased such that it refers to the next available spot in the array.

• All removing (dequeue) happens at index front

• Remove the element at index front

• Increment front

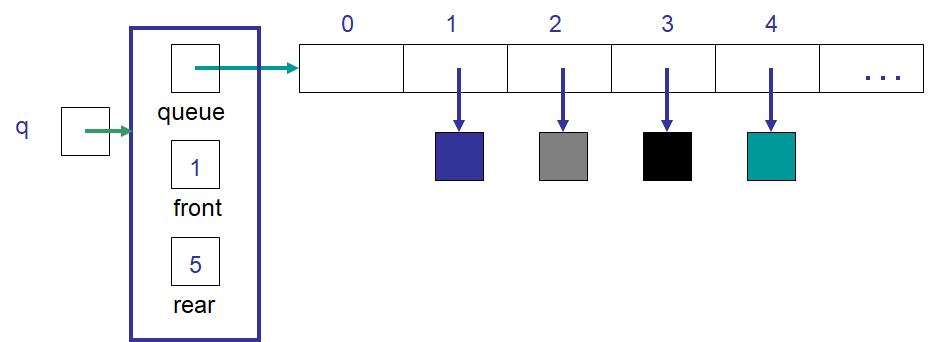
The state of idea #2’s ArrayQueue after an element was dequeued. Note that the element at index front was removed and the value of front increased by one. Note that, with the exception of the removed element, no other elements were required to be moved within the array.

15.2.1. Discussion

• Will this implementation work?

  • Is it correct?

• Knowing that this is an array implementation, will something like an expandCapacity be required?

• What is the computational complexity of an enqueue with this idea?

  • Amortized \(O(1)\)

• What is the computational complexity of a dequeue with this idea?

  • \(O(1)\)

• The drawback of idea #2 is the wasted space caused by dequeue

  • All indices before front are wasted

  • expandCapacity would need to be called after \(n + 1\) enqueues despite the number of elements actually in the queue

15.3. Idea #3

• Use an array for the container

• Keep track of the front index

• Keep track of the rear index

• Keep track of the size

• If there are empty indices before the front, wrap the rear back to 0 when the end of the array is hit

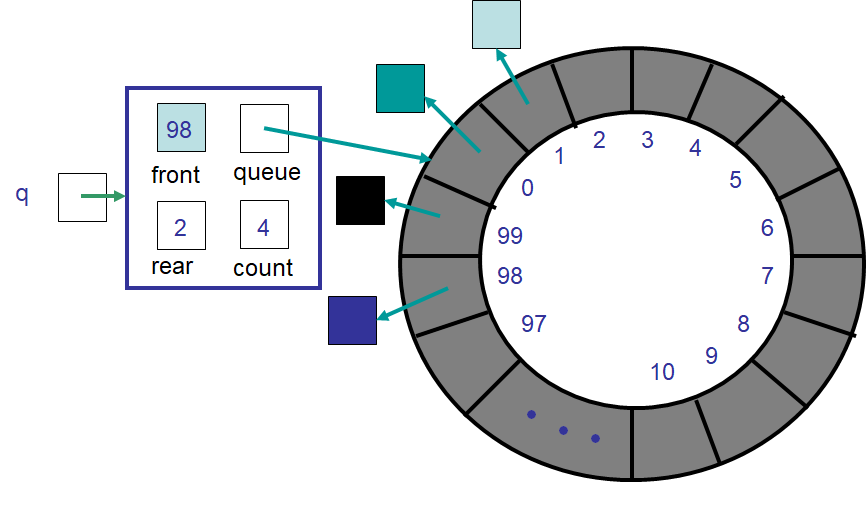
An example of idea #3’s ArrayQueue containing four elements. Note that the rear index has wrapped back to the beginning of the “circular” array.

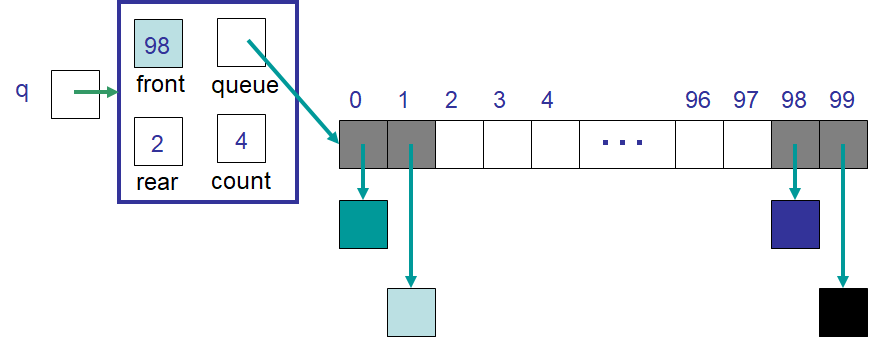
An example of idea #3’s ArrayQueue containing four elements. This figure contains the same ArrayQueue shown in the previous figure but with the “circular” array shown as a typical linear array.

15.3.1. “Circular” Array

• Pretend the array is a circle

  • The array is still, in reality, a linear array

• For example, given an array with a capacity of n

• The indices’ order would be

  ..., 0, 1, 2, 3, ..., n-2, n-1, 0, 1, 2, 3, ..., n-2, n-1, 0, 1, 2, 3, ...

• The index that comes after n-1 is 0

• The index that comes before 0 is n-1

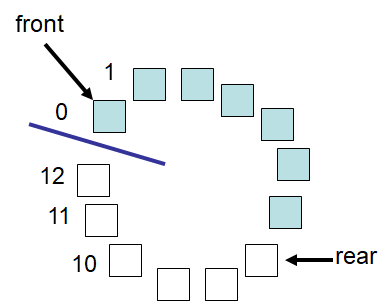
Example “circular” array with a capacity of 13. This figure shows the array containing seven elements stored in indices 0 – 6. Within the context of the ArrayQueue, front would be index 0 and rear would be 7.

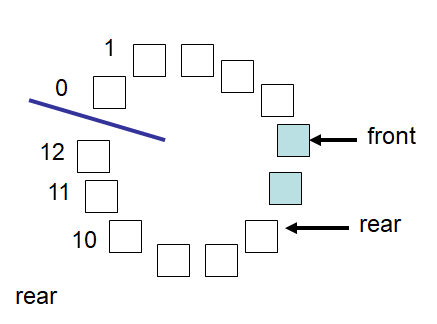
Example “circular” array with a capacity of 13 containing two elements stored in indices 5 and 6. This would be the state of the ArrayQueue shown in the proceeding figure after dequeue is called five times.

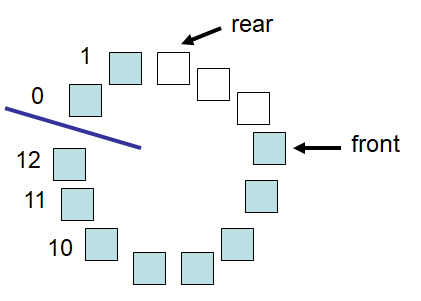
Example “circular” array with a capacity of 13 containing 10 elements stored in indices 5 – 12, 0 and 1. This would be the state of the ArrayQueue shown in the proceeding figure after enqueue is called eight times. Notice that rear wrapped back to the beginning of the array.

15.3.2. Modulo — %

• The modulo (%) operator provides a way to get the remainder of a division

  • 4 % 2

    • 4/2 == 2 remainder 0

    • Therefore, 4 % 2 is 0

  • 5 % 4

    • 5/4 == 1 remainder 1

    • Therefore, 5 % 4 is 1

  • 7 % 8

    • 7/8 == 0 remainder 7

    • Therefore, 7 % 8 is 7

• Knowing the remainder provides a way to wrap back to the beginning of an array

15.3.2.1. rear = (rear + 1) % queue.length

• Assume an array with a capacity 10

• Also assume rear is currently 9

• rear should always be the index of the next available spot in the array

• If enqueue is called, the new element is added to index 9 and rear is updated

• However, rear cannot simply be incremented to 10 since there is no index 10 in an array of capacity 10

• Instead, in this case, rear should be updated to 0

• This could be achieved with an if statement — if (rear == queue.length) rear = 0

• But notice that when rear == queue.length, rear % queue.length is 0

• But also notice that when rear is another number, like 4, rear % queue.length would be 4

• With this information, the following expression for incrementing the rear should make sense

  rear = (rear + 1) % queue.length

• If rear is 9 and this idea is used, rear will end up being (9 + 1) % 10 == 10 % 10 == 0

• If rear is any other number < 10, the number is not divisible by 10 and the % will make no difference

15.3.3. Discussion

• Does the strategy for updating front need to also be changed?

• Will this “circular” array ever run out of room?

Warning

Sometimes, good enough is good enough.

With this ArrayQueue implementation scenario, idea #3 is quite clearly the superior option and is not overly difficult to implement. However, as one continues in computer science and works on more complex problems, sometimes ease of implementation and maintainability becomes very important.

Better algorithms always exist, but a subpar implementation may do the trick, especially when the problem space is small enough that performance doesn’t matter.

Computational complexity is very important, but sometimes in practice one may lose the forrest through the trees. If an algorithm can be changed from \(O(n^{2})\) to \(O(n)\), then do it. But then again, if the updated algorithm will take a day to implement and it only needs to be run once on a small problem, perhaps \(O(n^{2})\) is good enough.

Even worse, trying to save a few FLOPS here and there is great and all, but if that’s distracting someone from other more important issues, perhaps they should move on.

Donald Knuth, a very famous computer scientist, says:

Programmers waste enormous amounts of time thinking about, or worrying about, the speed of noncritical parts of their programs, and these attempts at efficiency actually have a strong negative impact when debugging and maintenance are considered. We should forget about small efficiencies, say about 97% of the time: premature optimization is the root of all evil. Yet we should not pass up our opportunities in that critical 3%.

15.3.4. Expand Capacity

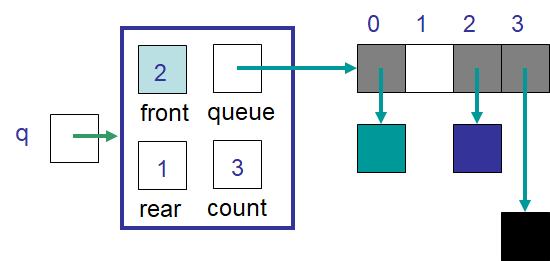
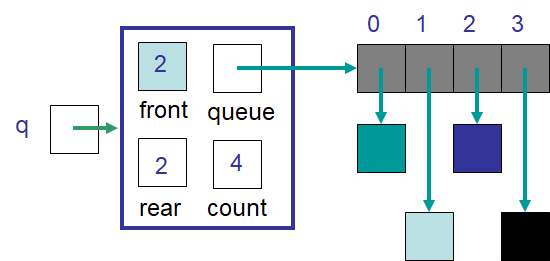
Example ArrayQueue with an array of capacity four containing three elements. The value of rear is 1 as it is the next available spot in the array.

Example ArrayQueue after a single element was added. The value of rear is 2 as it would be the next available spot in the array, however, the array is at capacity — size == queue.length.

• With an ArrayQueue at capacity, some expandCapacity method would need to be called

• Unlike before, however, the size of the array cannot simply just be doubled with the contents copied

  • See the aside on expandCapacity

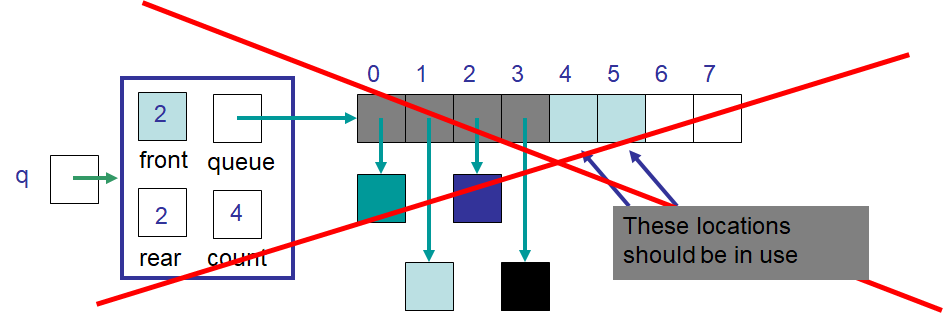
Example ArrayQueue after a naive expandCapacity. In this scenario, there is a “hole” in the middle of the elements as the front is index 2 and the elements wrapped back to the beginning of the array.

• Instead, copy the contents into contiguous indices starting at index front

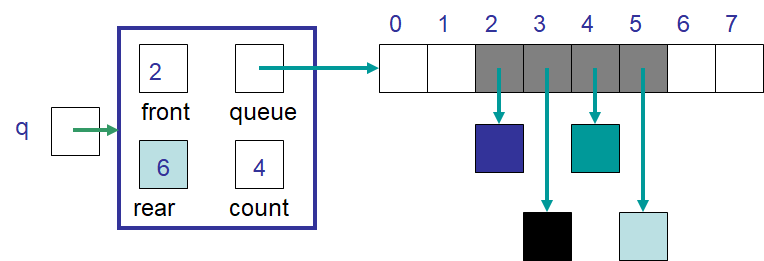
Example ArrayQueue with an improved expandCapacity. The elements are copied starting at index front.

• Another alternative is to copy the contents into contiguous indices starting at the beginning (index 0) of the new array

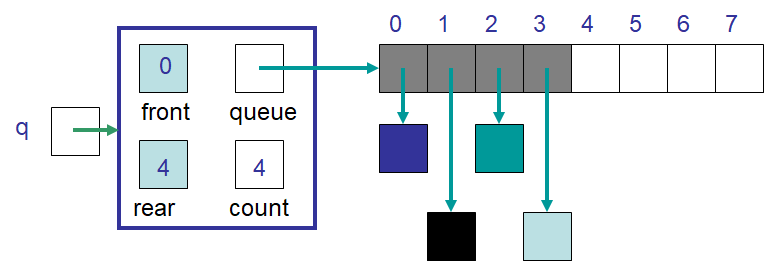
Example ArrayQueue with another improved expandCapacity. These elements are copied by starting at index front in the old array and copying them starting at index 0 in the new array.

15.3.5. Discussion Again

• Will this implementation work?

  • Is it correct?

• What is the computational complexity of this enqueue?

• What is the computational complexity of this dequeue?

• How often will this call expandCapacity relative to idea #1 and #2?

15.4. Implementing a Queue — Array Container

• All the code is available for download at the bottom of the page

• Here, only a subset of methods are shown

15.4.1. enqueue

    @Override
    public boolean enqueue(T element) {
        if (size == queue.length) {
            queue = expandCapacity(queue);
        }
        queue[rear] = element;
        rear = nextIndex(rear);
        size++;
        return true;
    }

• Note the call to expandCapacity and nextIndex

    /**
     * Calculates the next valid index for the front or rear fields. This method is used to have the index increment
     * with an automatic wrapping back to index zero if there is no more room left at the end of the array.
     *
     * @param currentIndex Index to find next index of
     * @return Wrapping next index
     */
    private int nextIndex(int currentIndex) {
        return (currentIndex + 1) % queue.length;
    }

• nextIndex is a simple private helper method to return the next index for a “circular” array

    /**
     * Returns a new array with double the size of the queue array container and copy the contents from the old array to
     * the new array. Note that the elements are copied to the beginning (index 0) of the new array and the front and
     * rear fields are updated.
     */
    @SuppressWarnings("unchecked")
    private T[] expandCapacity(T[] oldQueue) {
        T[] newQueue = (T[]) new Object[oldQueue.length * 2];
        for (int i = 0; i < oldQueue.length; i++) {
            newQueue[i] = oldQueue[front];
            front = nextIndex(front);
        }
        front = 0;
        rear = size();
        return newQueue;
    }

• The expandCapacity used here is different from earlier versions

• First, notice that the copying is from index front to i

  • Previously, for the ArrayStack, newStack[i] = oldStack[i]

• Each time the loop updates both i and front

  • front is updated with nextIndex

• After all the copying is complete, the front for the newQueue is set to 0

• rear is set to the size

  • When front is 0, rear must be equal to size

15.4.2. dequeue

    @Override
    public T dequeue() {
        if (isEmpty()) {
            throw new NoSuchElementException("Empty queue");
        }
        T returnElement = queue[front];
        front = nextIndex(front);
        size--;
        return returnElement;
    }

• Since front may wrap around to index 0, the private method nextIndex is used

15.4.3. equals

    @Override
    public final boolean equals(Object o) {
        if (this == o) {
            return true;
        }
        if (o == null || getClass() != o.getClass()) {
            return false;
        }
        ArrayQueue<?> that = (ArrayQueue<?>) o;
        if (this.size() != that.size()) {
            return false;
        }
        int thisCurrentIndex = this.front;
        int thatCurrentIndex = that.front;
        // Since this and that are the same size, this.size() can be used safely in the for loop
        for (int i = 0; i < this.size(); i++) {
            if (!Objects.equals(this.queue[thisCurrentIndex], that.queue[thatCurrentIndex])) {
                return false;
            }
            thisCurrentIndex = this.nextIndex(thisCurrentIndex);
            thatCurrentIndex = that.nextIndex(thatCurrentIndex);
        }
        return true;
    }

• It does not matter where in the array the contents are

• It also does not matter what the capacities of the arrays are

• All that matters is that the elements in the two arrays are equivalent

  • Starting at their respective front indices and wrapping when necessary

15.5. For Next Time

• See the aside on expandCapacity

• Read Chapter 5 Section 7

  • 7 pages

15.5.1. Playing Code

• Download and play with

  • ArrayQueue code

  • ArrayQueueTest tests

  • ArrayQueue playing code

• One could use the same code from PlayingLinkedQueue to play with the ArrayQueue

• Only need to make one change

  • LinkedQueue -> ArrayQueue

• If everything was done correctly, the following code from PlayingArrayQueue should work

import java.util.NoSuchElementException;

public class PlayingArrayQueue {
    public static void main(String[] args) {
        // Create a ArrayQueue
        Queue<Integer> myQueue = new ArrayQueue<>(5);

        // Check queue is empty
        System.out.println(myQueue.size());
        System.out.println(myQueue.isEmpty());
        System.out.println(myQueue);

        // Test enqueue
        myQueue.enqueue(0);
        myQueue.enqueue(1);
        myQueue.enqueue(2);
        myQueue.enqueue(3);
        myQueue.enqueue(4);
        System.out.println(myQueue.size());
        System.out.println(myQueue.isEmpty());
        System.out.println(myQueue);

        // Test enqueue more to check expandCapacity
        myQueue.enqueue(10);
        myQueue.enqueue(11);
        myQueue.enqueue(12);
        myQueue.enqueue(13);
        myQueue.enqueue(14);
        System.out.println(myQueue.size());
        System.out.println(myQueue.isEmpty());
        System.out.println(myQueue);

        // Test first
        System.out.println(myQueue.first());
        System.out.println(myQueue.size());
        System.out.println(myQueue.isEmpty());
        System.out.println(myQueue);

        // Test dequeue
        System.out.println(myQueue.dequeue());
        System.out.println(myQueue.dequeue());
        System.out.println(myQueue.dequeue());
        System.out.println(myQueue.dequeue());
        System.out.println(myQueue.dequeue());
        System.out.println(myQueue.dequeue());
        System.out.println(myQueue.dequeue());
        System.out.println(myQueue.dequeue());
        System.out.println(myQueue.dequeue());
        System.out.println(myQueue.dequeue());
        System.out.println(myQueue.size());
        System.out.println(myQueue.isEmpty());
        System.out.println(myQueue);

        // Test first and dequeue throwing exception
        try {
            myQueue.first();
        } catch (NoSuchElementException e) {
            e.printStackTrace();
        }
        try {
            myQueue.dequeue();
        } catch (NoSuchElementException e) {
            e.printStackTrace();
        }
    }
}