18. Bag Implementations

  • Given the definition of a Bag

  • And given the definitions of the specialized bags

    • IndexedBag

    • SortedBag

  • How can they be implemented?

18.1. Array Implementation Idea

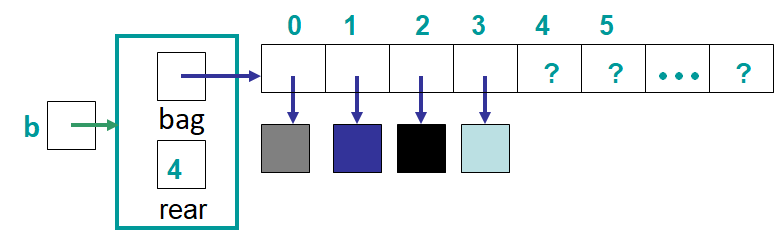
../../_images/array_bag.png

A representation of how a Bag could be implemented with an array.

  • The idea will be similar to the Stack and Queue array based implementations

  • Unlike a Queue, the front will always be at index 0

    • With bags, adding and removing can happen anywhere

    • Adding to the middle would require a linear time operation to make room

    • Removing from the middle would require a linear time operation to eliminate the gap

  • An expandCapacity will be required

    • The simpler version though since the front is always index 0

  • The functionality of a Bag, regardless of what specific version it is

    • boolean add(T element)

    • boolean remove(T element)

    • boolean contains(T element)

    • int count(T element)

    • boolean isEmpty()

    • int size()

    • Iterator<T> iterator()

18.2. ArrayIndexedBag

  • In addition to the functionality of the Bag, an IndexedBag must also be able to

    • boolean add(int index, T element)

    • T remove(int index)

    • T set(int index, T element)

    • T get(int index)

    • int indexOf(T element)

Note

For brevity, only a subset of methods are included below. See the ArrayIndexedBag class for the full implementation.

 7/**
 8 * Implementation of an IndexedBag with an array as the container. The array container will automatically "grow" to
 9 * accommodate adding beyond the initial capacity.
10 *
11 * @param <T> Type of elements that are to be in the IndexedBag
12 */
13public class ArrayIndexedBag<T> implements IndexedBag<T> {
14
15    private static final int DEFAULT_CAPACITY = 100;
16    private static final int NOT_FOUND = -1;
17    private T[] bag;
18    private int rear;
19
20    /**
21     * Create an empty ArrayIndexedBag of the default capacity.
22     */
23    public ArrayIndexedBag() {
24        this(DEFAULT_CAPACITY);
25    }
26
27    /**
28     * Create an empty ArrayIndexedBag with the specified capacity.
29     *
30     * @param initialCapacity Starting capacity of the fixed length array
31     */
32    @SuppressWarnings("unchecked")
33    public ArrayIndexedBag(int initialCapacity) {
34        bag = (T[]) new Object[initialCapacity];
35        rear = 0;
36    }

  • Note the import of Iterator and the implementation of Iterator<T>

    • Iterators are used for iterating over a collection

    • More on this later

18.2.1. Private Methods

41    /**
42     * Shifts elements in an array down (towards index 0) to the starting index specified. The element at the starting
43     * index will be overwritten.
44     *
45     * @param start Index of element to be overwritten and where shifting moves down to
46     */
47    private void shiftLeft(int start) {
48        for (int i = start; i < rear - 1; i++) {
49            bag[i] = bag[i + 1];
50        }
51        bag[rear - 1] = null;
52    }
53
54    /**
55     * Shifts elements in an array up (towards index rear) away from the starting index specified. The array location
56     * at the specified starting index will be open. This method assumes there is room in the array to facilitate the
57     * shifting.
58     *
59     * @param start Index of where the array has a new open location and where shifting moves up from
60     */
61    private void shiftRight(int start) {
62        for (int i = rear; i > start; i--) {
63            bag[i] = bag[i - 1];
64        }
65        bag[start] = null;
66    }

  • shiftLeft and shiftRight

    • These move elements up or down the array to make or eliminate room for adding and removing elements

18.2.2. Iterator Method

Warning

Iterators are the focus of another topic, so they are only briefly presented here.

  • Iterators are used to provide a common way to iterator over a collection, regardless of the underlying container

    • Array vs. linked structure

186    @Override
187    public Iterator<T> iterator() {
188        return new ArrayIterator<>(bag, size());
189    }

  • All this method does is create an instance of an ArrayIterator and return it

  • What the ArrayIterator class looks like is discussed later in the course

18.2.3. Add Methods

 89    @Override
 90    public boolean add(T element) {
 91        return add(rear, element);
 92    }
 93
 94    @Override
 95    public boolean add(int index, T element) {
 96        // Index == size() is valid as that just appends
 97        if (index < 0 || index > size()) {
 98            throw new IndexOutOfBoundsException(index);
 99        }
100        if (size() == bag.length) {
101            bag = Arrays.copyOf(bag, bag.length * 2);
102        }
103        shiftRight(index);
104        bag[index] = element;
105        rear++;
106        return true;
107    }

  • Note that add(T element) simply delegates to add(int index, T element) for ease and code/logic reuse

  • Unlike the methods for adding to a Stack or Queue, this method may throw an exception

    • The exception is thrown if the specified index is out of bounds

  • Like the Stack and Queue, the array may run out of space

  • Unlike before, an expandCapacity method is not included

  • Instead, the copyOf function from the Arrays class is used

    • It creates a new array with the specified capacity containing a copy of the elements in the original array

  • The shiftRight private method is used to make room for the element to be added

18.2.4. Remove

129    @Override
130    public T remove(int index) {
131        if (index < 0 || index >= size()) {
132            throw new IndexOutOfBoundsException(index);
133        }
134        T returnElement = bag[index];
135        shiftLeft(index);
136        rear--;
137        return returnElement;
138    }
139
140    @Override
141    public boolean remove(T element) {
142        if (!contains(element)) {
143            return false;
144        }
145        int removeIndex = indexOf(element);
146        remove(removeIndex);
147        return true;
148    }

  • The remove(T element) method delegates to the remove(int index) for ease and code/logic reuse

18.3. ArraySortedBag

  • In addition to the functionality of the Bag, a SortedBag must also be able to

    • T removeFirst()

    • T removeLast()

    • T first()

    • T last()

  • Further, the overloaded add and remove methods must preserve the ordering of the elements

Note

For brevity, only a subset of methods are included below. See the ArraySortedBag class for the full implementation.

 7/**
 8 * Implementation of a SortedBag with an array as the container. The array container will automatically "grow" to
 9 * accommodate adding beyond the initial capacity.
10 *
11 * @param <T> Type of elements that are to be in the SortedBag
12 */
13public class ArraySortedBag<T extends Comparable<? super T>> implements SortedBag<T> {
14
15    private static final int DEFAULT_CAPACITY = 100;
16    private static final int NOT_FOUND = -1;
17    private T[] bag;
18    private int rear;
19
20    /**
21     * Create an empty ArraySortedBag of the default capacity.
22     */
23    public ArraySortedBag() {
24        this(DEFAULT_CAPACITY);
25    }
26
27    /**
28     * Create an empty ArraySortedBag with the specified capacity.
29     *
30     * @param initialCapacity Starting capacity of the fixed length array
31     */
32    @SuppressWarnings("unchecked")
33    public ArraySortedBag(int initialCapacity) {
34        bag = (T[]) new Comparable[initialCapacity];
35        rear = 0;
36    }

  • Notice <T extends Comparable<? super T>>

  • There is a little bit to unpack here

  • First, when something extends Comparable, it means that the type has some defined ordering

    • The method compareTo is implemented for the type

  • If x.compareTo(y) is called

    • Return a negative integer if x < y

    • Return zero if x == y

    • Return a positive integer if x > y

  • When something extends Comparable<T>, that means this can be compared to some type T

    • this can be compared to things of type T, but not the other way around

  • T extends Comparable<T> means that the type T can be compared to things of type T to provide some defined ordering

    • Which is needed, if the elements are to be sorted

  • Finally, <T extends Comparable<? super T>> means that T can be compared to something of type T or a superclass of T

    • ? is a wildcard

  • Thus, this means that T must have a defined ordering for itself through either

    • A direct implementation of compareTo

    • Inheritance

18.3.1. Adding Method

 88    @Override
 89    public boolean add(T element) {
 90        if (size() == bag.length) {
 91            bag = Arrays.copyOf(bag, bag.length * 2);
 92        }
 93        int insertIndex = findInsertIndex(element);
 94        shiftRight(insertIndex);
 95        bag[insertIndex] = element;
 96        rear++;
 97        return true;
 98    }
 99
100    /**
101     * Linear search through the bag to find the index of where the element should be inserted. If equal elements
102     * exist within the collection, the returned index will be after the existing equal elements.
103     *
104     * @param element Item to be inserted
105     * @return Index where the element should be inserted
106     */
107    private int findInsertIndex(T element) {
108        int searchIndex = 0;
109        for (T bagElement : this) {
110            if (element.compareTo(bagElement) <= 0) {
111                return searchIndex;
112            }
113            searchIndex++;
114        }
115        // Element must belong at rear
116        return rear;
117    }

  • The add method makes use of a private method findInsertIndex

  • findInsertIndex makes use of the class’ iterator method to iterate over the collection

    • It is simply used to perform a linear search

  • It also makes use of the compareTo method

  • Remember, the elements themselves determine the ordering

    • One does not know what the type T is, so how can they be compared?

      • If they’re numbers, <, >, ==, would work

      • But what if sorting strings? Colours?

  • Since T must have a compareTo implemented, it can be used to guarantee a proper ordering, regardless of the type

    • T must have a compareTo since it must extend Comparable<? super T>

  • Given this, the loop executes until it finds the index where the element to be inserted is less than the current element in the collection

    • Or, in other words, it loops while

      • There are more elements in the collection

      • The thing to be inserted belongs after the current element in the collection

18.4. Linked Implementation

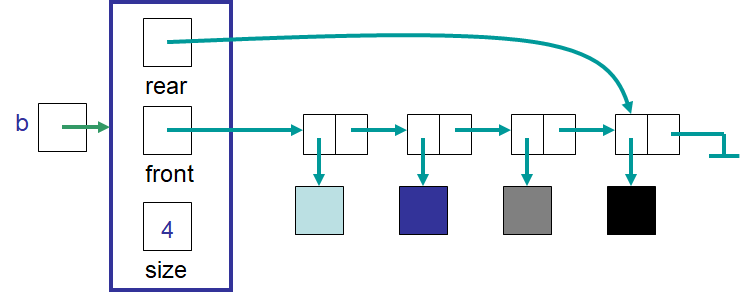
../../_images/linked_bag.png

A representation of how a Bag could be implemented with a linked structure.

18.5. For Next Time

Note

Note that there are better implementations of these data structures. One will be discussed later in the course.

  • Read Chapter 6 Sections 6 & 7

    • 17 pages

18.5.1. Playing Code