23. Searching

• For the purposes of this topic, searching is the process of looking for a specified thing in some collection to know if it exists within the collection

• For example, does a given number exist within an array of numbers?

• To write an algorithm to solve this problem, all that’s needed is something that says if it’s there or not

  • That’s all that’s required

  • Any algorithm that works would suffice

• However, the focus here will be on two intuitive ideas that people commonly use in one way or another throughout their lives

  • Linear Search

  • Interpolation Search

    • A specific kind of interpolation search called a binary search will be discussed

• Throughout this topic

  • The thing being searched for will be referred to as the needle

  • The collection being searched through will be referred to as the haystack

23.1. Linear Search

• Start at the beginning of the haystack and sequentially look at each element until the needle is found

  • If the needle is found, then conclude that it is there

  • If the end of the haystack is reached without finding the needle, then conclude that it is not there

• Notice that this description of the algorithm doesn’t go into any more details

  • It is fairly high-level — abstract

• The computational complexity of this algorithm is linear — \(O(n)\)

  • Worst case scenario, every element in the haystack was looked at before making any conclusion — linear \(O(n)\)

  • Best case scenario, the needle is the first element in the haystack — constant \(O(1)\)

  • On average, the element will be in the middle — linear \(O(n)\)

    • For every time needle is the first element, it could be the last element in another search

    • For every time the needle is the second element, it could be in the second last position in another search

    • …

Example linear collection of data. With a linear search, to guarantee if some needle exists within this haystack, each element must be looked at.

23.1.1. Iterative

• Below is a generic implementation of a linear search on an array of type T

    public static <T> int iterativeLinearSearch(T needle, T[] haystack) {
        for (int i = 0; i < haystack.length; i++) {
            if (Objects.equals(haystack[i], needle)) {
                return i;
            }
        }
        return NOT_FOUND;
    }

• This iterative implementation is fairly similar to the high-level description of the algorithm

  • Start at i = 0 — the beginning of the haystack

  • If the element at index i is the needle, conclude that it’s there

  • Otherwise continue and increment i

  • If the end of the haystack is reached without finding the needle, then conclude that it is not there

23.1.2. Recursive

• Below is a recursive implementation of a linear search following the same high-level abstract idea

    public static <T> int recursiveLinearSearch(T needle, T[] haystack, int currentIndex) {
        if (currentIndex == haystack.length) {
            return NOT_FOUND;
        } else if (Objects.equals(haystack[currentIndex], needle)) {
            return currentIndex;
        } else {
            return recursiveLinearSearch(needle, haystack, currentIndex + 1);
        }
    }

• If I wanted to call this method, I would start with currentIndex as 0

  • recursiveLinearSearch(someNeedle, someHaystack, 0)

• This may seem quite different from the iterative implementation, but the high-level idea is the same

  • Start currentIndex at 0

  • If the end of the haystack is reached without finding the needle, then conclude that it is not there

  • If the element at index currentIndex is the needle, conclude that it’s there

  • Otherwise continue by calling the recursive function again with currentIndex incremented

23.2. Binary Search

• Imagine looking for page 554 in a roughly 1000 page textbook

• It would be reasonable to start by opening the textbook somewhere in the middle-ish

• If the page landed on was page 402, which half of the book must page 554 be in?

  • Left set of pages, or right set of pages?

• Since 554 is greater than 402, it must be in the right set of pages

  • This means, after looking at a single page, the 401 pages in the left set can be ignored

• With this information, imagine turning to another page in the right set of pages and landing on page 621

  • Which remaining set of pages must the page 554 be in?

  • In the left set of pages (403 – 620), or the right set (622 – 1000)?

• This general idea is the basis of binary search

  • Technically, this is interpolation search

  • A binary search is a special kind of interpolation search

• There is, however, a catch with binary search when compared to a linear search

• The haystack being searched must be sorted

• If it was not sorted, it would not be possible to conclude which half the needle is in after investigating an element

• The complexity analysis of binary search may feel intimidating, but the trick is to visualize the work being done

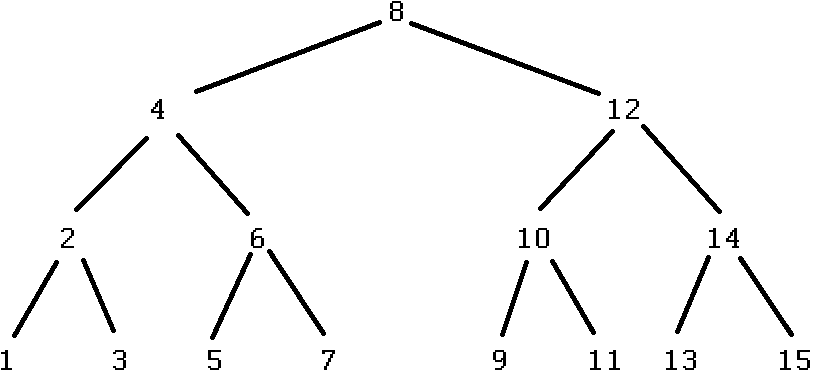
Visualization of how to search for a number within the range 1 – 15. The initial guess would be the halfway point and each subsequent guess would be the halfway point of the remaining elements. Elements at the bottom would take 4 guesses to find.

• To analyze the complexity, consider the worst case scenario

  • Look for an element at the bottom as it would take the most number of guesses to find

  • Looking for an element that does not exist would also work

• First, imagine performing a linear search where the needle is 15

• In this case, all \(15\) elements in the haystack would need to be investigated before the needle was found

  • Since it is at the end of the haystack

• When considering a binary search, how many things would need to be looked at before 15 is found?

  • \(4\)

  • 8 -> 12 -> 14 -> 15

• The reason this takes fewer steps is because roughly half of the remaining elements are ignored after each check

  • For example, 15 is greater than 8, therefore the numbers 1 – 7 can be ignored

  • In other words, with linear search, after a single guess, only the element checked can be eliminated

  • But with binary search, the element checked, plus roughly half the remaining elements, can be ignored

• There is a relationship between the maximum number of checks and the number of elements \(n\) in the haystack

  • \(n = 2^{h + 1} - 1\), where h is the “height” of the “tree”, or, the number of steps needed to get from the top to the bottom

  • \(h = log_{2}(n + 1) - 1\)

• Thus, the computational complexity of binary search is \(O(log_{2}(n))\)

  • As \(n\) grows, the maximum number of steps that could be taken grows like \(log_{2}(n)\)

Warning

The above explanation uses details not discussed in this course yet, but they be covered in subsequent topics. In other words, don’t be too concerned if these ideas are not 100% clear yet.

23.2.1. Iterative

• Below is a generic implementation of an iterative binary search

  • Take note that T or one of their superclasses must extend Comparable

  • This is because the elements must be ordered

    public static <T extends Comparable<? super T>> int iterativeBinarySearch(T needle, T[] haystack) {
        int lowIndex = 0;
        int highIndex = haystack.length;
        int midpoint = (highIndex - lowIndex) / 2;

        while (lowIndex < highIndex) {
            if (haystack[midpoint].compareTo(needle) == 0) {
                return midpoint;
            } else if (Objects.compare(haystack[midpoint], needle, T::compareTo) > 0) {
                highIndex = midpoint - 1;
                midpoint = lowIndex + (highIndex - lowIndex) / 2;
            } else {
                lowIndex = midpoint + 1;
                midpoint = lowIndex + (highIndex - lowIndex) / 2;
            }
        }
        return NOT_FOUND;
    }

• Here is what’s happening

  • While search space has not been exausted (lowIndex < highIndex)

    • If lowIndex is ever greater than or equal to highIndex, there are no more indices the element could exist

  • Look at the middle

  • If the element in the middle is the needle

    • Done

  • If the element in the middle is less than the needle

    • Continue the search on the remaining upper half by looking at the midpoint of the remaining elements

  • If the element in the middle is greater than the needle

    • Continue the search on the remaining lower half by looking at the midpoint of the remaining elements

23.2.2. Recursive

• Below is a recursive implementation of a binary search

• Notice that, other than being recursive, the underlying high-level algorithm is the same as the iterative implementation

    public static <T extends Comparable<? super T>> int recursiveBinarySearch(T needle, T[] haystack, int lowIndex, int highIndex) {
        if (lowIndex >= highIndex) {
            return NOT_FOUND;
        }
        int midpoint = lowIndex + (highIndex - lowIndex) / 2;
        if (haystack[midpoint].compareTo(needle) == 0) {
            return midpoint;
        } else if (Objects.compare(haystack[midpoint], needle, T::compareTo) > 0) {
            return recursiveBinarySearch(needle, haystack, lowIndex, midpoint - 1);
        } else {
            return recursiveBinarySearch(needle, haystack, midpoint + 1, highIndex);
        }
    }

• To call this method to initiate a search, start with lowIndex as 0 and highIndex as someHaystack.length

  • recursiveBinarySearch(someNeedle, someHaystack, 0, someHaystack.length)

23.3. For Next Time

• Read Chapter 9 Section 1

  • 7 pages

23.3.1. Playing Code

• Download and play with

  • SearchingFunctions

  • SearchingFunctionsTest