24. Tree ADT

  • Trees are nonlinear data structures

    • The data does not naturally arrange in an obvious linear, sequential way

  • Trees are useful when organizing data in some hierarchical way

    • Family trees

    • Inheritance

    • File systems on a computer

    • Decision trees

    • Table of contents of a book

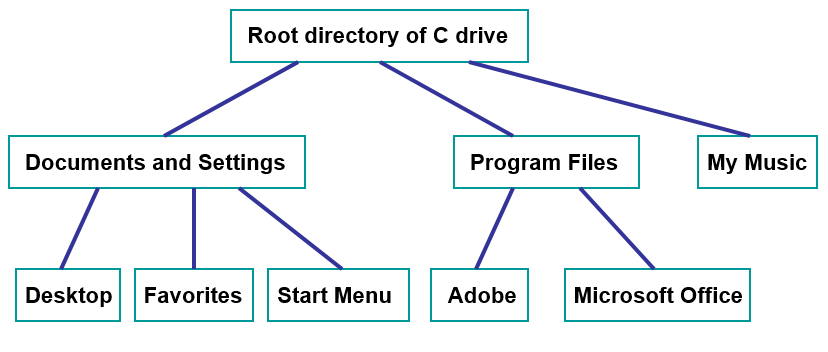
../../_images/tree_example.png

A simple file system on a computer.

24.1. Definitions & Terminology

24.1.1. Tree Definition

  • A tree is a collection of elements such that:

    • It is empty

    • Or, it has a special element called the root, from which descends zero or more trees (subtrees)

  • Notice that this definition is recursive

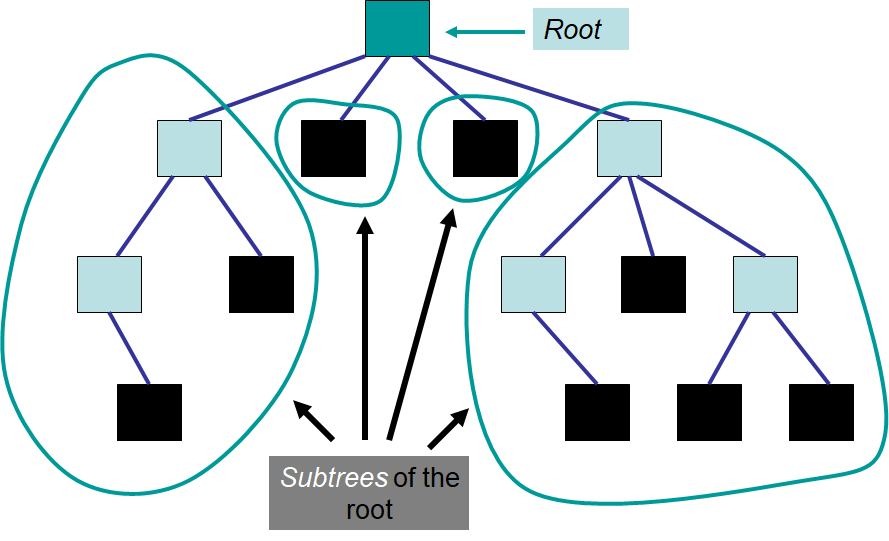
../../_images/tree_definition.png

Example of an arbitrary tree with subtrees identified. The root element has four existing subtrees. Each of these subtrees has a root with zero or many descending subtrees.

24.1.2. Nodes

  • A node is a single entity in the tree

  • An edge connects nodes

  • The root node is a special element that is the origin of the tree

    • A tree can have one or zero root nodes

  • A leaf node is a node without an edge to a child node

  • An interior node is not a leaf node

  • An empty tree is a tree with no nodes or edges

    • This is still a tree based on the definition of the tree discussed above

    • Think empty stack/queue/bag — they still exist, but they’re just empty

Warning

It is possible to find alternative definitions of trees; however, the definition included here is used as it is common.

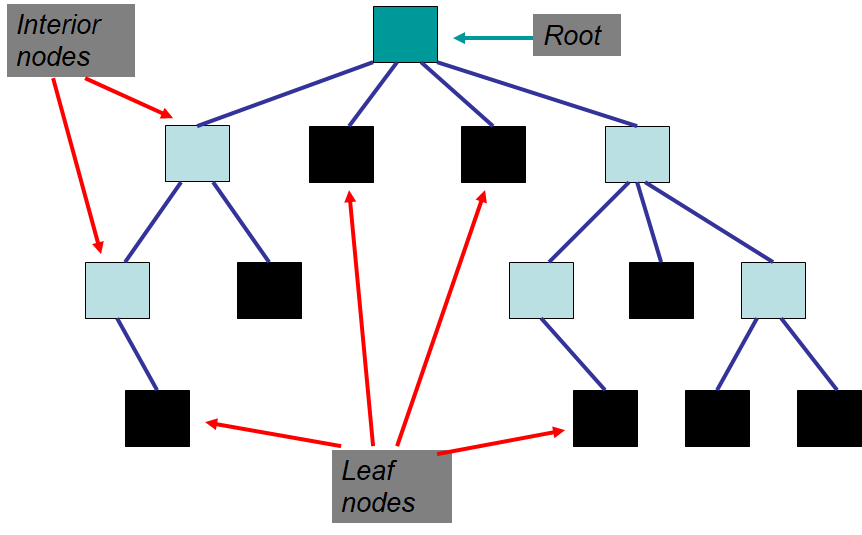
../../_images/tree_nodes.png

Tree with nodes labelled as a root, interior, or leaf node. In this example, there are six interior nodes, including the root, and eight leaf nodes.

24.1.3. Relationships

  • A parent/predecessor of a given node is the node directly above in the hierarchy

    • Each node can have at most one parent, except for the root, which has no parent

  • A child/successor of a given node is the node directly below in the hierarchy

    • Each node can have any number of children

  • A sibling of a given node is a node that has the same parent

  • An ancestor of a given node is the parent, or the parent’s parent, or …

  • A descendant of a given node is the child, or the child’s child, or …

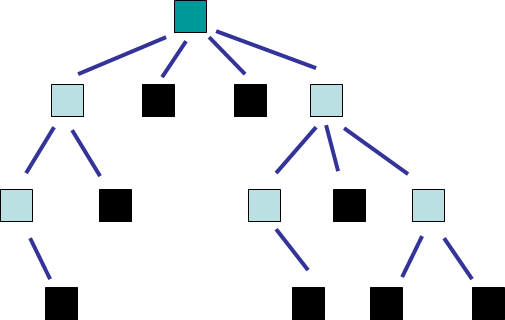
../../_images/tree_base.png

Example of an arbitrary tree.

  • Observations

    • A leaf node cannot have any children

    • The root node of the whole tree has no parent node

    • With the exception of the root node, each node has exactly one parent

  • A subtree of a given node is a child node and all descendants

    • A subtree is itself a tree

    • A node may have many subtrees

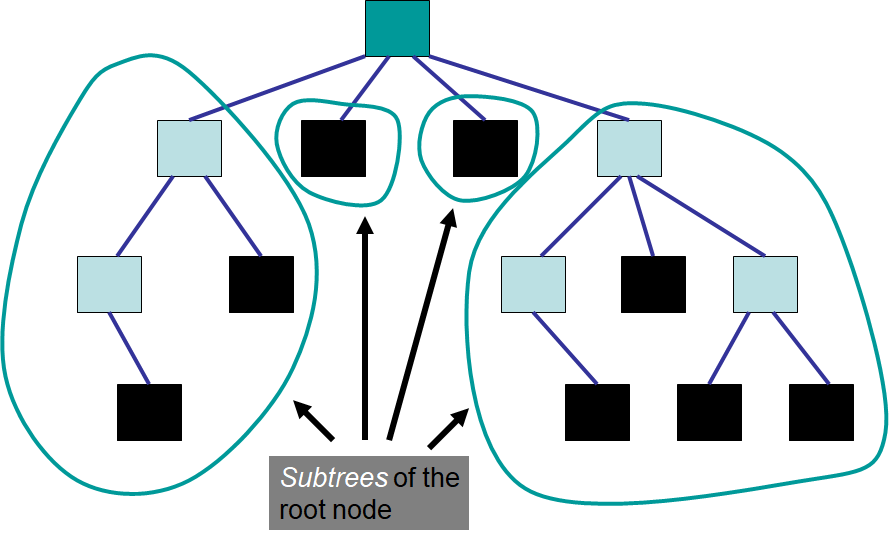
../../_images/tree_subtrees.png

Tree with the subtrees of the root node identified.

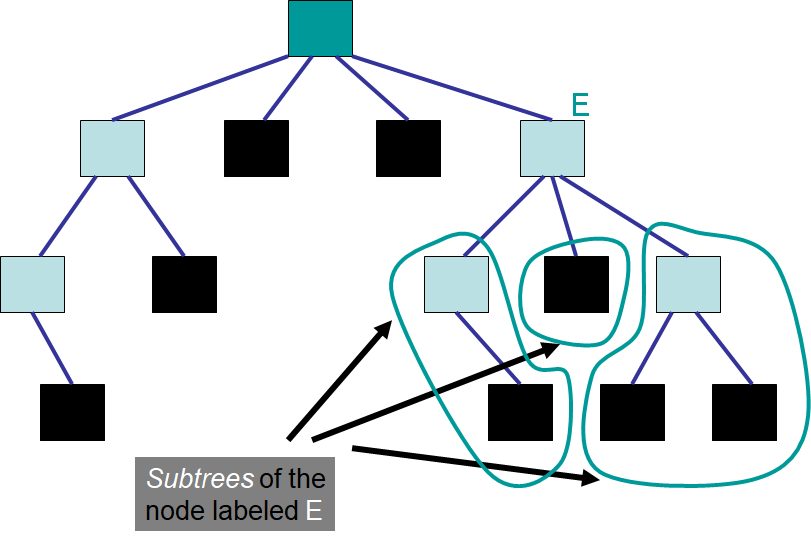
../../_images/tree_subtree_root.png

Tree with the subtrees of the node labelled “E” identified.

24.1.4. Properties

  • A path is the sequence of nodes and edges leading from one node to another

  • The path length is the number of edges in the path

  • The level of a given node is the number of edges between the root and the node

    • Recursive definition

      • The level of the root is 0

      • The level of a node that is not the root is the level of its parent + 1

  • The height of a tree is the number of levels the tree has

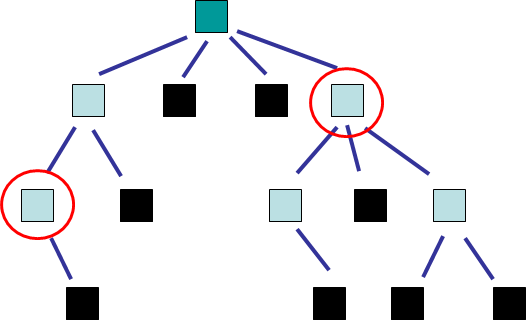
../../_images/tree_path.png

Tree with two nodes emphasized.

  • Observations

    • The path length between the two emphasized nodes is three (3)

    • The height of this tree is three (3)

    • A tree with only a root has a height of zero (0)

    • The height of an empty tree is negative one (-1)

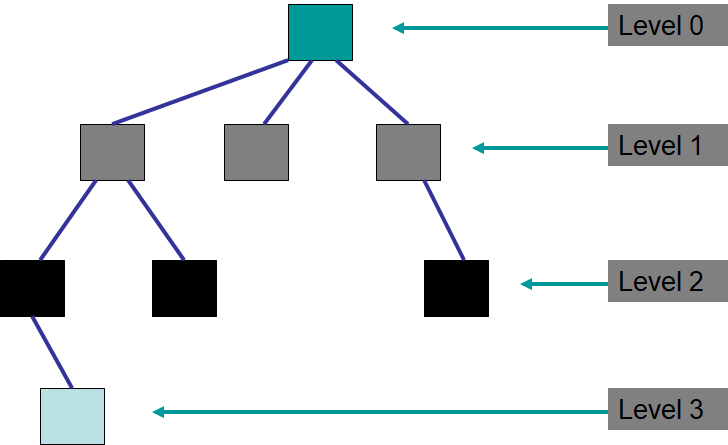
../../_images/tree_levels.png

Tree with three levels. This tree has a height of three (3).

  • The degree/arity of a given node is the number of children the node has

  • The degree/arity of a tree is the maximum degree/arity of the tree’s nodes

24.2. For Next Time

  • Read Chapter 10 Sections 1 – 3

    • 10 pages