25. Binary Trees

  • A general tree is one where each node can have any number of children

  • An n-ary tree is one where each node has no more than \(n\) children

25.1. Binary Tree Definition

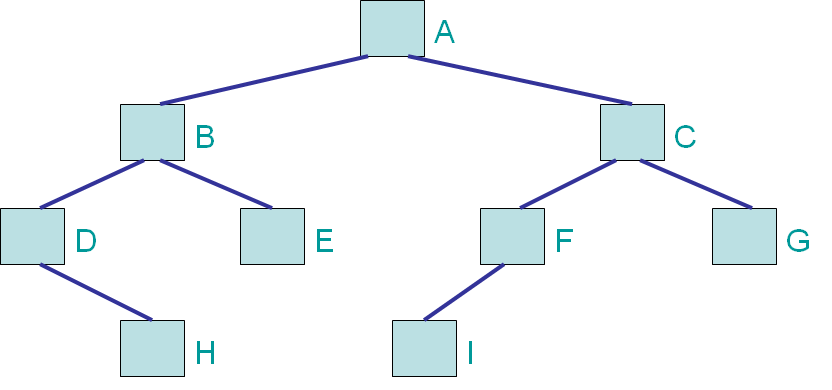
../../_images/binary_tree_example.png

Binary tree containing nine (9) nodes. Each node has no more than two (2) children. The left/right position of child nodes is important for binary trees.

  • A binary tree is one where each node has no more than two (2) children

    • 2-ary tree

    • Tree with a degree/arity of 2

  • If a node has children, they are referred to as the left and right children

    • Which are also referred to as the left and right subtrees

    • In the above example, B is the left subtree and C is the right subtree of A

  • In a binary tree, position matters

    • It matters if a subtree is the left or right

  • A recursive definition of a binary tree is

    • An empty tree

    • Or, a tree that has a root whose left and right subtrees are binary trees

Note

Based on this information, what would a unary tree be?

25.2. Traversals

../../_images/example1.png

A linear linked structure of singly linked nodes.

  • With a simple linear structure, the order in which the nodes are traversed is rather natural

    • Start at one end and go to the other

    • For example, start at the head node and visit each node’s next until there are no more nodes

  • Other traversal orders could be defined for linear collections if desired, but that would be atypical

../../_images/binary_tree_example.png

A nonlinear linked structure — a binary tree.

  • With a nonlinear data structure like a binary tree, the order to traverse the nodes in is not immediately obvious

  • There are a few common options to choose from

25.2.1. Pre-order

  • A pre-order traversal is a common order to traverse a binary tree

  • The general idea is

    • Start at the root

    • Access the node, then go to the left child, then the right child

  • To get more precise in a recursive definition

1Define PreOrderTraversal
2    If the node exists
3        Access the node
4        Call PreOrderTraversal on the left child node
5        Call PreOrderTraversal on the right child node

  • Notice that the root of the (sub)tree is accessed before (pre-) any recursive calls

../../_images/binary_tree_example.png

A pre-order traversal of the binary tree would visit the nodes in the order A, B, D, H, E, C, F, I, G.

25.2.2. In-order

  • An in-order traversal is another common traversal

  • The general idea is

    • Start at the root

    • Go to the left child, Access the node, then the right child

  • To get more precise in a recursive definition

1Define InOrderTraversal
2    If the node exists
3        Call InOrderTraversal on the left child node
4        Access the node
5        Call InOrderTraversal on the right child node

  • Notice that the root of the (sub)tree is accessed in between any recursive calls

../../_images/binary_tree_example.png

An in-order traversal of the binary tree would visit the nodes in the order D, H, B, E, A, I, F, C, G

25.2.3. Post-order

  • Take a wild guess at what this one will be

  • A post-order traversal is another traversal

  • The general idea is

    • Start at the root

    • Go to the left child, then the right child, then Access the node,

  • To get more precise in a recursive definition

1Define PostOrderTraversal
2    If the node exists
3        Call PostOrderTraversal on the left child node
4        Call PostOrderTraversal on the right child node
5        Access the node

  • Notice that the root of the (sub)tree is accessed after (post-) any recursive calls

../../_images/binary_tree_example.png

A post-order traversal of the binary tree would visit the nodes in the order H, D, E, B, I, F, G, C, A.

25.2.4. Level-order

  • A level-order traversal is a little different when compared to the others

  • The search doesn’t work it’s way down each branch of the tree one by one

  • Instead, it traverses the breadth of the tree on the way down all branches

  • The idea is

    • Start at the root

    • Visit the nodes in each level from left to right

  • With this idea, there is no immediately obvious recursive definition of this traversal

  • An iterative definition of the traversal is perhaps simpler to derive

 1Define LevelOrderTraversal
 2    If the root node exists
 3        Enqueue the root node to a queue
 4
 5    While the queue is not empty
 6        Dequeue a node
 7        Access the dequeued node
 8
 9        If the left child exists
10            Enqueue the left child to the queue
11
12        If the right child exists
13            Enqueue the right child to the queue
../../_images/binary_tree_example.png

A level-order traversal of the binary tree would visit the nodes in the order A, B, C, D, E, F, G, H, I.

25.2.5. Iterative Pre/In/Post-Order

  • With the iterative level-order traversal, a queue was used

  • What would happen if a stack was used?

  • With the recursive pre-/in-/post-order traversals, a stack was used

    • The call stack

    • No directly instantiated stack data structure was used, but one could have been used

  • How would the level-order traversal need to be changed to do a pre-/in-/post-order traversal?

25.2.6. Traversal Analysis

../../_images/binary_tree_example.png

A nonlinear linked structure — a binary tree.

  • Consider a binary tree with \(n\) nodes

  • If all \(n\) nodes are to be visited, what is the computational complexity of

    • pre-order traversal?

    • in-order traversal?

    • post-order traversal?

    • level-order traversal?

  • Intuitively, they’re all \(O(n)\) since all \(n\) nodes must be visited once and only once

  • If the question was changed slightly, consider a binary tree with height \(h\)

    • What is the computational complexity of the traversals?

    • Consider the relationship between the height of a binary tree and the number of nodes within the tree

    • \(O(2^{h})\)

25.3. Interface

  • What would a binary tree need to do?

    • Check if an element exists in the tree

    • Count the number of occurrences of a given element

    • Check if its empty

    • Get the size

    • Traverse the tree

    • Add elements

      • But where?

    • Remove elements

      • Which one, from where?

  • Adding/removing something to a stack and queue was more straightforward

    • Pushing and popping happened at the top of the stack

    • Enqueuing and dequeueing happen at opposite ends

  • For a binary tree, with add and remove, what is wanted/what it means will depend on the type of binary tree

  • Similar to the bag, elements must be able to be added and removed from the binary tree

  • But what what exactly add and remove means may differ depending on the specific type of binary tree

 1import java.util.Iterator;
 2import java.util.NoSuchElementException;
 3
 4public interface BinaryTree<T> extends Iterable<T> {
 5
 6    boolean add(T element);
 7    boolean remove(T element);
 8    boolean contains(T element);
 9    int count(T target);
10    boolean isEmpty();
11    int size();
12    Iterator<T> iterator();
13    Iterator<T> preOrderIterator();
14    Iterator<T> inOrderIterator();
15    Iterator<T> postOrderIterator();
16    Iterator<T> levelOrderIterator();
17}

25.4. Linked Implementation

  • No binary tree implementation is being created; it will be inherited from for specific binary tree implementations

    • For example, a BinarySearchTree

  • One way to implement a binary tree is with a collection of linked nodes

  • Use a size field to keep track of the number of elements within the tree

  • Use a field to reference the root node

    • Like how a reference was used to keep track of the top of a stack or the front of a queue

25.4.1. Binary Tree Node

  • Until now, the node class has only had a single successor

  • However, there is no rule saying that there can’t be more than one successor

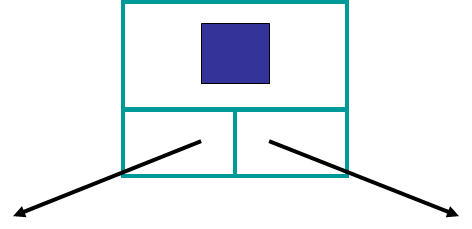
../../_images/binary_tree_node.png

Example node containing data and references to two successor nodes. These successors are referred to as left and right.

  • Here, have the node contain:

    • A reference to some element

    • A reference to a left child

    • A reference to a right child

  • A new Node a standalone class, but this may cause confusion between singly linked nodes and nodes with two successors

  • A simple way to address this is to make the Node class a static nested class inside the specific BinaryTree implementation

462    /**
463     * A node class for a linked binary tree structure. Each node contains a nullable reference to data of type T, and a
464     * reference to the left and right child nodes, which may be null references.
465     *
466     * @param <T> Type of the data being stored in the node
467     */
468    private static class Node<T> {
469        private T data;
470        private Node<T> left;
471        private Node<T> right;
472
473        private Node() {
474            this(null);
475        }
476
477        private Node(T data) {
478            this.data = data;
479            this.left = null;
480            this.right = null;
481        }
482
483        private T getData() {
484            return data;
485        }
486
487        private void setData(T data) {
488            this.data = data;
489        }
490
491        private Node<T> getLeft() {
492            return left;
493        }
494
495        private void setLeft(Node<T> left) {
496            this.left = left;
497        }
498
499        private Node<T> getRight() {
500            return right;
501        }
502
503        private void setRight(Node<T> right) {
504            this.right = right;
505        }
506    }

25.4.2. Linked Binary Tree

  • Although there will be no implementation of a general BinaryTree, general binary tree related methods can be discussed

25.4.2.1. size

  • Given some arbitrary binary tree with no size field, the number of elements can be counted recursively

    • If the current node exists, then the size of the (sub)tree it is the root of will be 1 + the size of the left subtree + the size of the right subtree

 1public int size() {
 2    return size(root);
 3}
 4
 5private int size(Node<T> current) {
 6    if (current == null) {
 7        return 0;
 8    } else {
 9        return 1 + size(current.getLeft()) + size(current.getRight());
10    }
11}

  • Here a public setup method is used to start the private recursive method call on the root

  • What is the computational complexity of this size() method?

    • \(O(n)\), where \(n\) is the number of nodes in the tree

25.4.2.2. contains

  • Given some arbitrary binary tree, a specific element can be searched for recursively

    • If the current element is what is being looking for, done

    • Otherwise, check the left subtree

    • If it wasn’t found in the left subtree, then check the right subtree

 1public boolean contains(T needle) {
 2    return contains(root, needle);
 3}
 4
 5private boolean contains(Node<T> current, T needle) {
 6    if (current == null) {
 7        return false;
 8    } else if (Objects.equals(current.getData(), needle)) {
 9        return true;
10    } else {
11        return contains(current.getLeft(), needle) || contains(current.getRight(), needle);
12    }
13}

  • Mind the use of the short-circuit or in the above example

  • What is the computational complexity of this contains() method?

    • \(O(n)\), where \(n\) is the number of nodes in the tree

    • Although the right subtree may not have been searched, the worst case scenario is considered

25.4.2.3. Traversals

  • Preorder traversal printing out the elements

 1public void preOrder() {
 2    preOrder(root);
 3}
 4
 5private void preOrder(Node<T> current) {
 6    if (current != null) {
 7        System.out.println(current.getData());
 8        preOrder(current.getLeft());
 9        preOrder(current.getRight());
10    }
11}

  • An inorder traversal, but instead of printing out the contents, add them to some other collection

 1public IndexedBag<T> inOrder() {
 2    IndexedBag<T> sequence = new ArrayIndexedBag<>();
 3    inOrder(root, sequence);
 4    return sequence;
 5}
 6
 7private void inOrder(Node<T> current, IndexedBag<T> sequence) {
 8    if (current != null) {
 9        inOrder(current.getLeft(), sequence);
10        sequence.add(current.getData());
11        inOrder(current.getRight(), sequence);
12    }
13}

25.5. For Next Time

  • Read Chapter 10 Sections 4 – 7

    • 34 pages (mostly code though)

25.5.1. Playing Code