2. Ant Colony Optimization (ACO)
Ant Colony Optimization (ACO) is a bio inspired optimization technique
Based on the foraging behavior of ant colonies, it mimics how ants find the shortest path to food
2.1. Ants!
Note
This “backyard” will help visualize the ACO
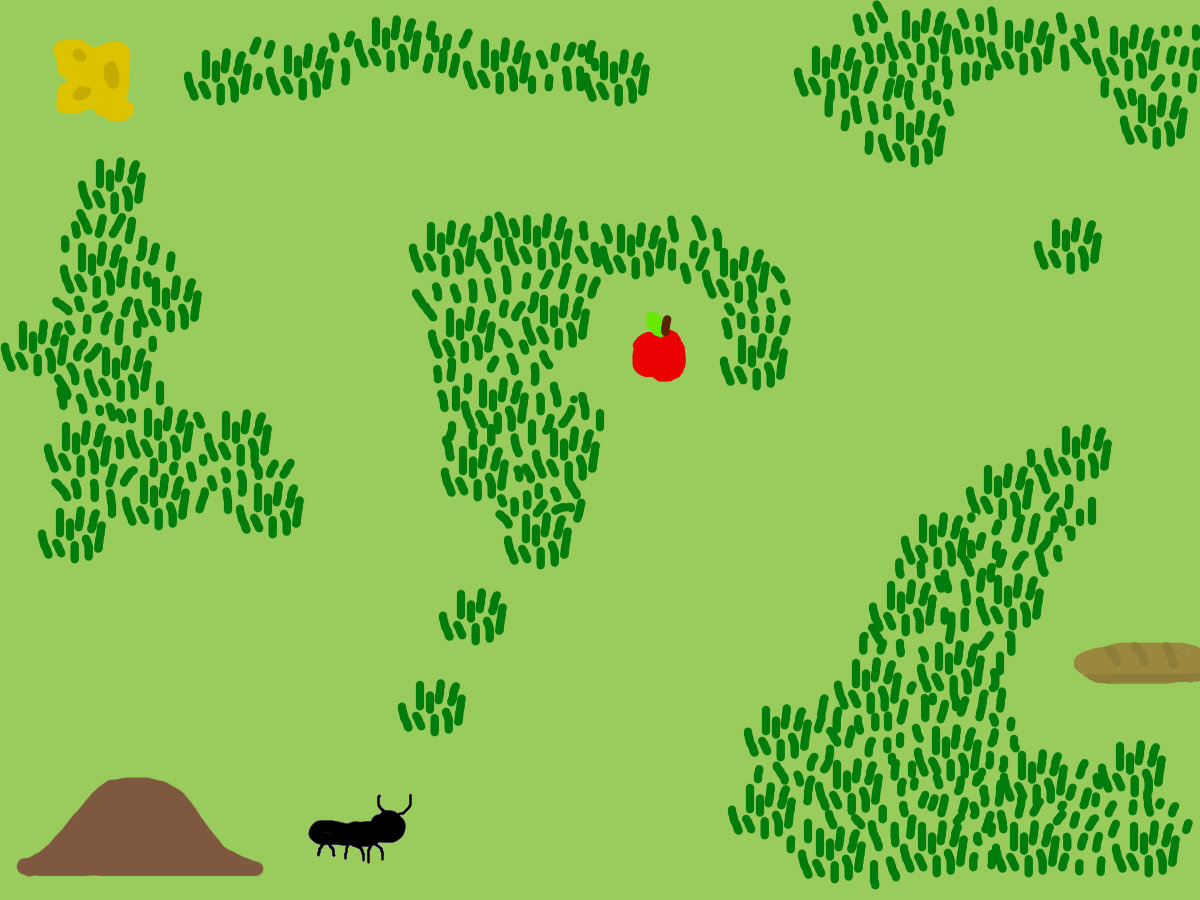
Ants leave pheromone trails as they travel to guide other ants
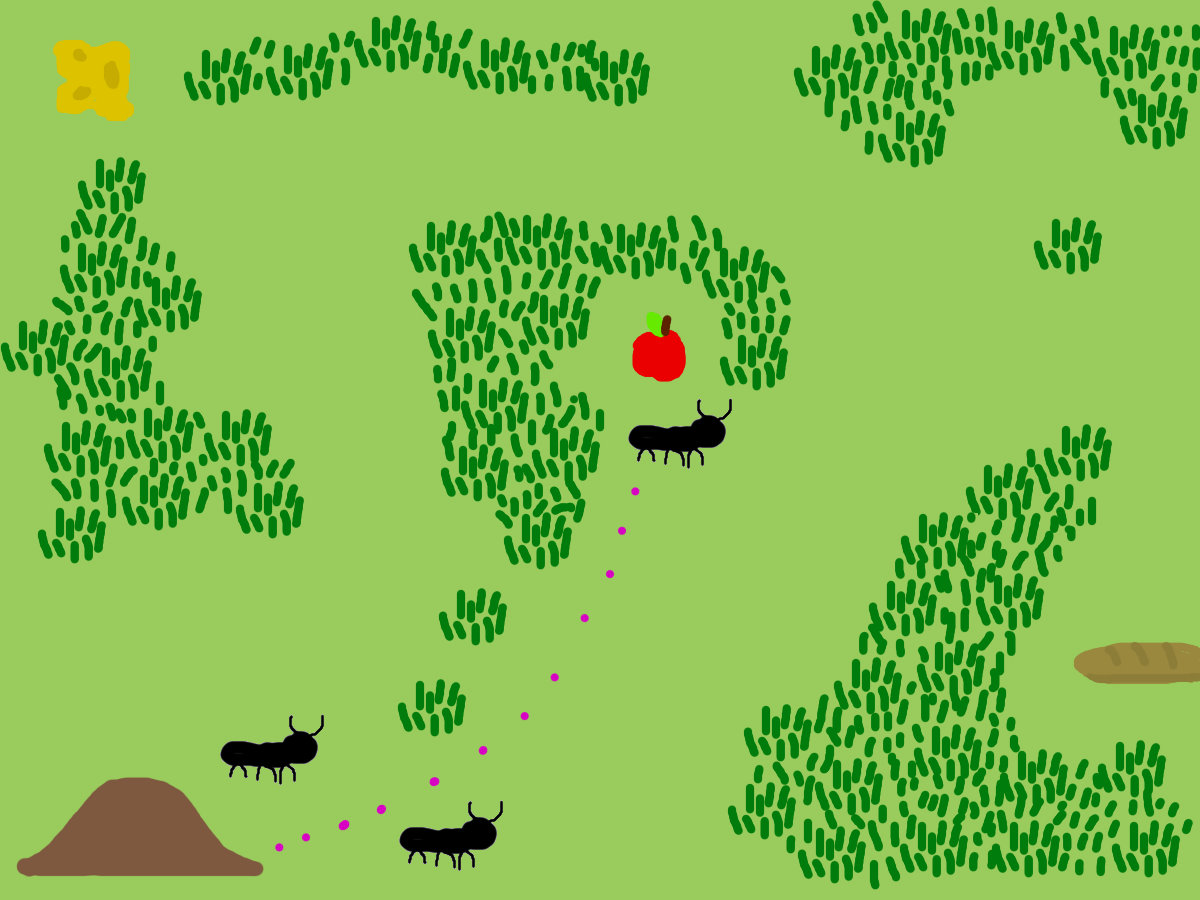
The other ants are attracted to the pheromones
more pheromones attract more ants reinforcing the shorter routes
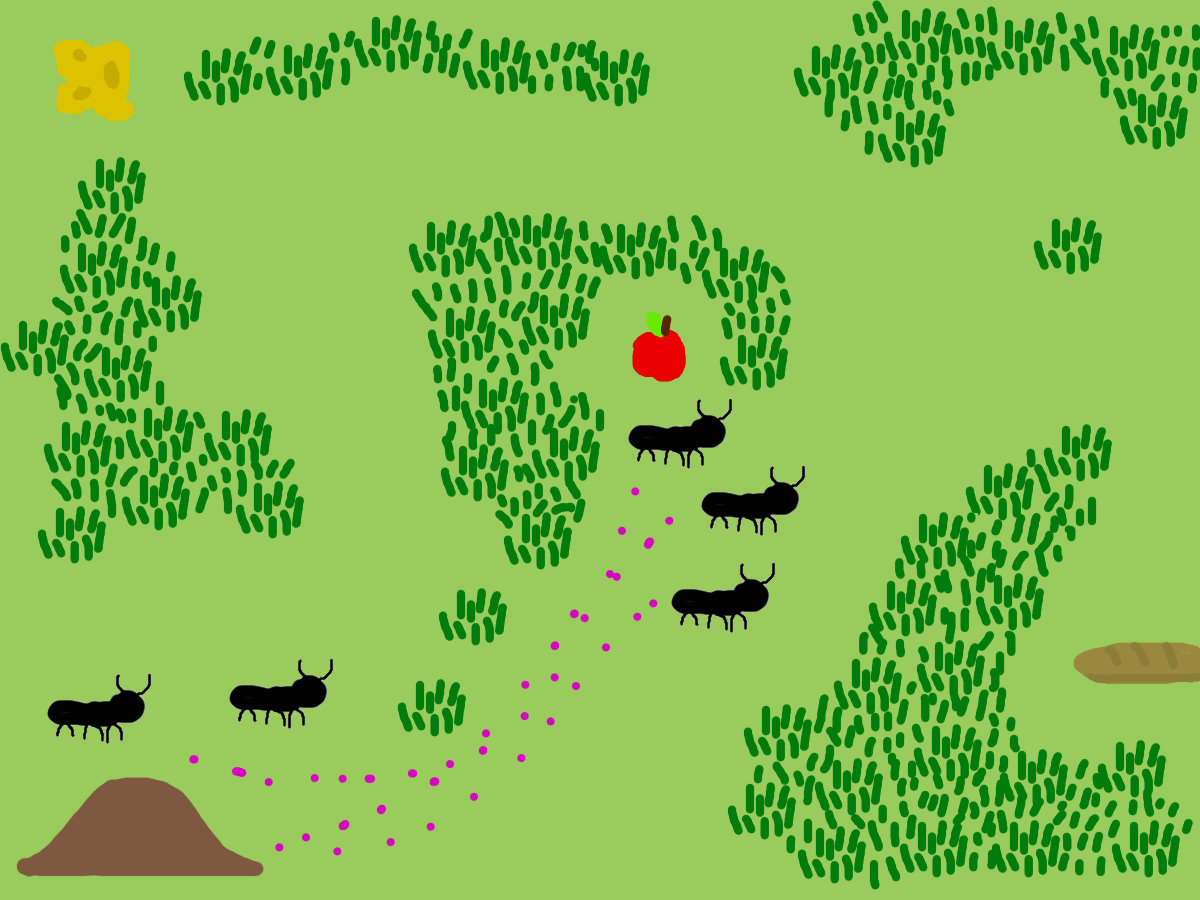
More pheromones accumulate on the shorter paths making them more favored by the ants
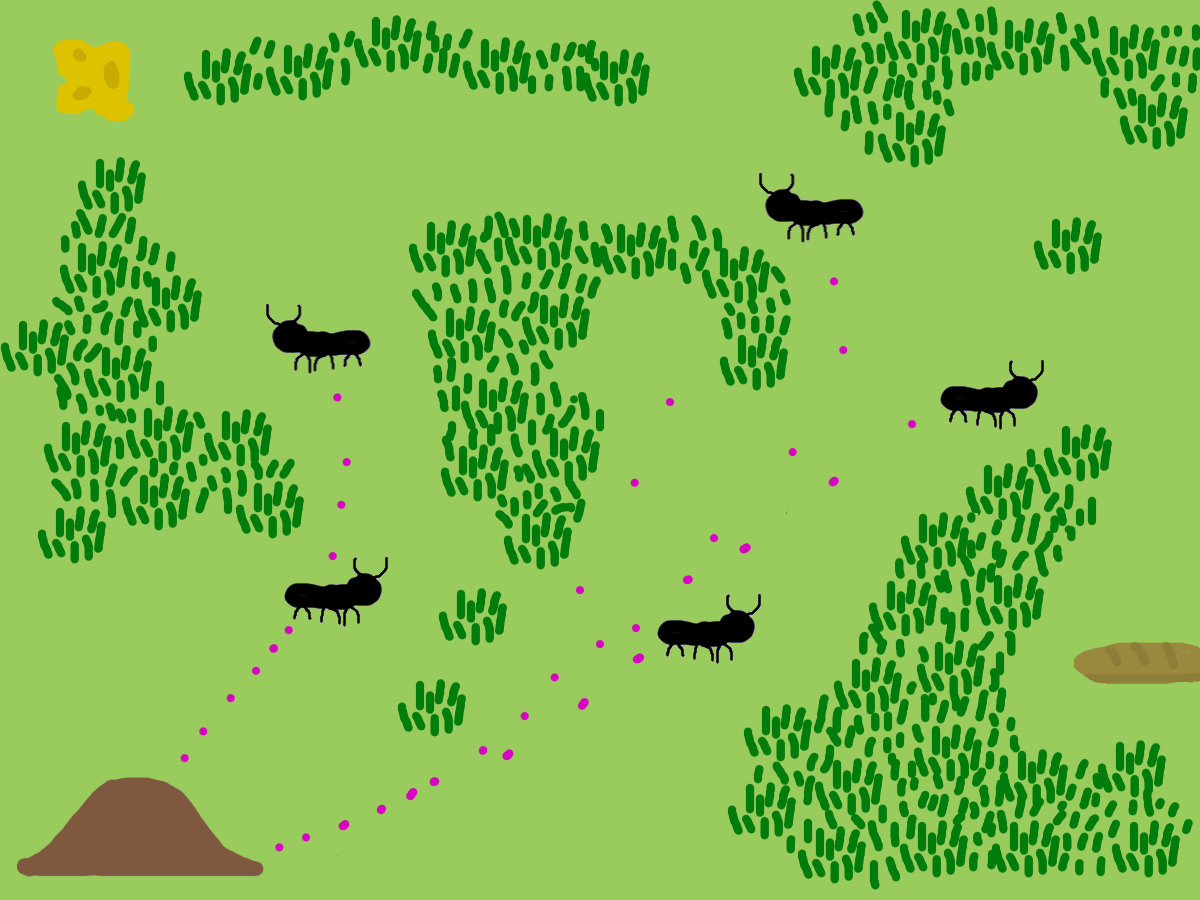
The longer it takes an ant to travel a path the more time the pheromones have to evaporate
Over time pheromone evaporate from paths
This allows for the exploration of newer alternative paths
2.2. Traveling SalesAnt Problem
The best way to understand this is to apply it to an already know problem like TSP
But this time the S stands fro SalesAnt

Now our back yard is a city and our ants are here to do some business
The goal is the same as in normal TSP, visit every city in the shortest route and return to start
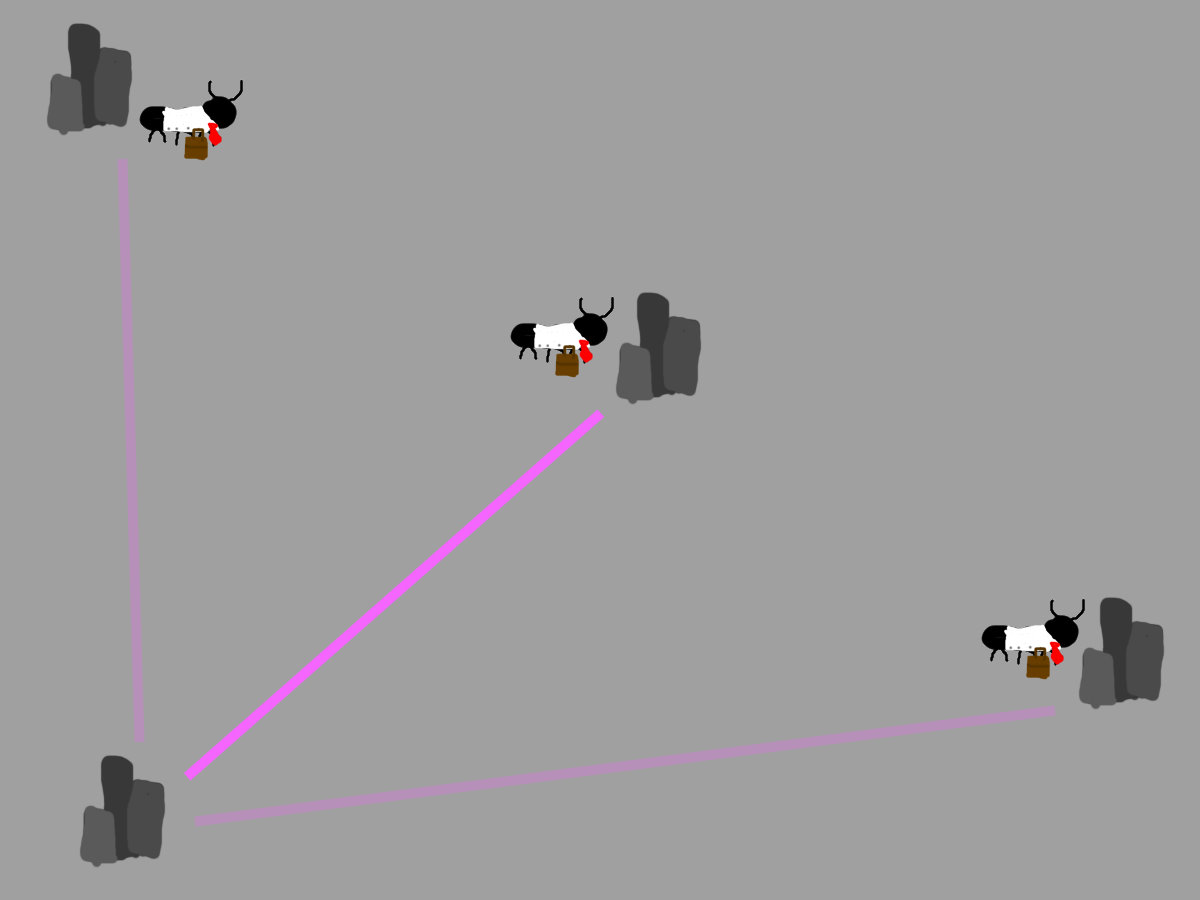
To start Ants wil travel to random locations
While traveling the ants will leave a pheromone trail,
the longer it took them to travel to the city the weaker the pheromones will be when the next ant detects them
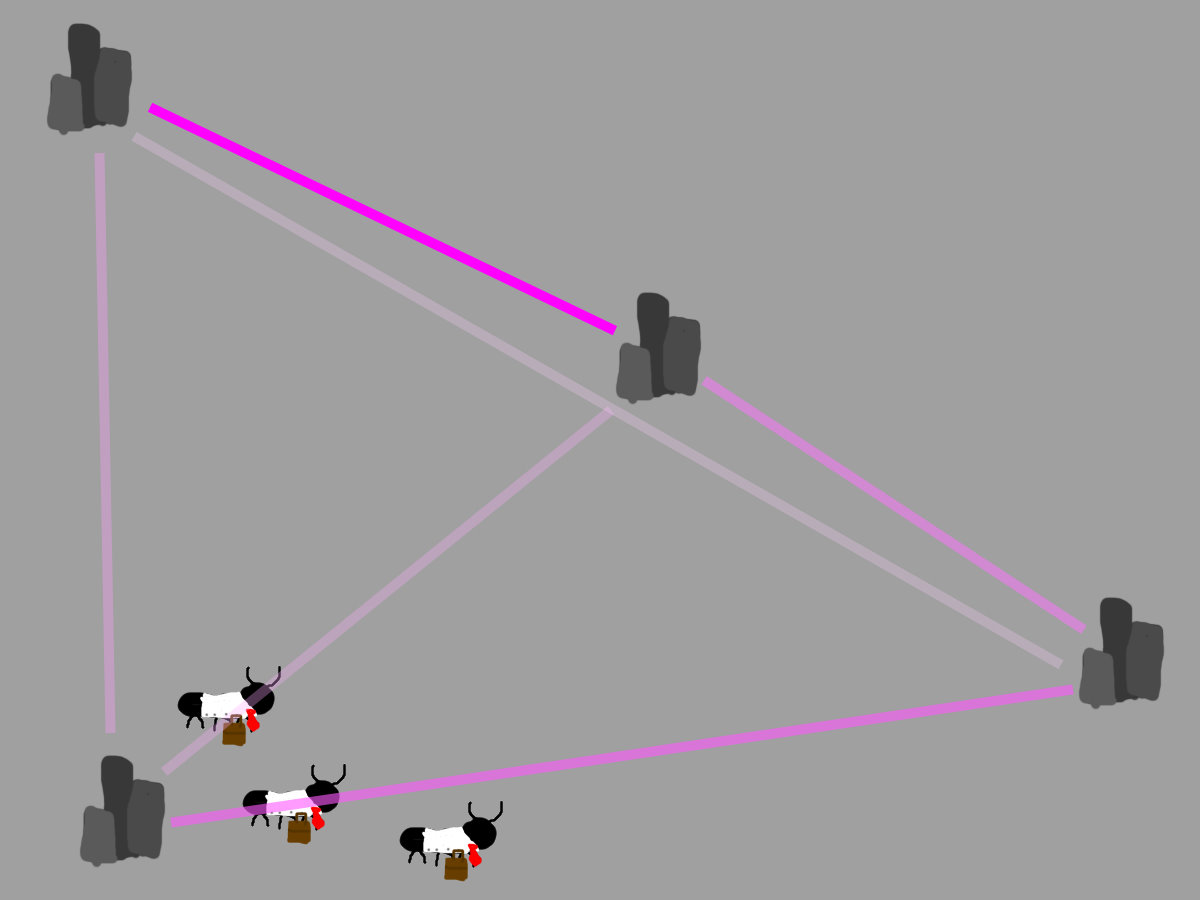
These starter ants will randomly finish their routes and return home
This sets up a base pheromone trail for the rest of the ants
The pheromone trail on the left has gotten stronger because multiple ants used it in their paths
The strength of a pheromone trail is determined by the following formula
\(\tau_{xy}\) is the amount of pheromone deposited from city \(x\) to city \(y\)
\(\rho\) is the pheromone evaporation coefficient
\(m\) is the number of ants who traversed the path from city \(x\) to city \(y\)
\(\Delta\tau_{xy}^k\) is the amount of pheromone deposited by the \(k\) th ant between city \(x\) to city \(y\)
In a TSP, the value of \(\Delta\tau_{xy}^k\) is determined by the how long the path is
For example:
\(\Delta \tau_{xy}^k =\begin{cases}\frac{Q}{L_k} & \text{if ant } k \text{ uses path } xy \text{ in its tour}\\0 & \text{otherwise}\end{cases}\)
\(Q\) is a constant
\(L_k\) is the distance between city \(x\) and city \(y\)
This function
update_pheromonesis an implementation of the formula above for pheromone depositionThe pheromone trails are updated once the current wave of ants have finished their paths
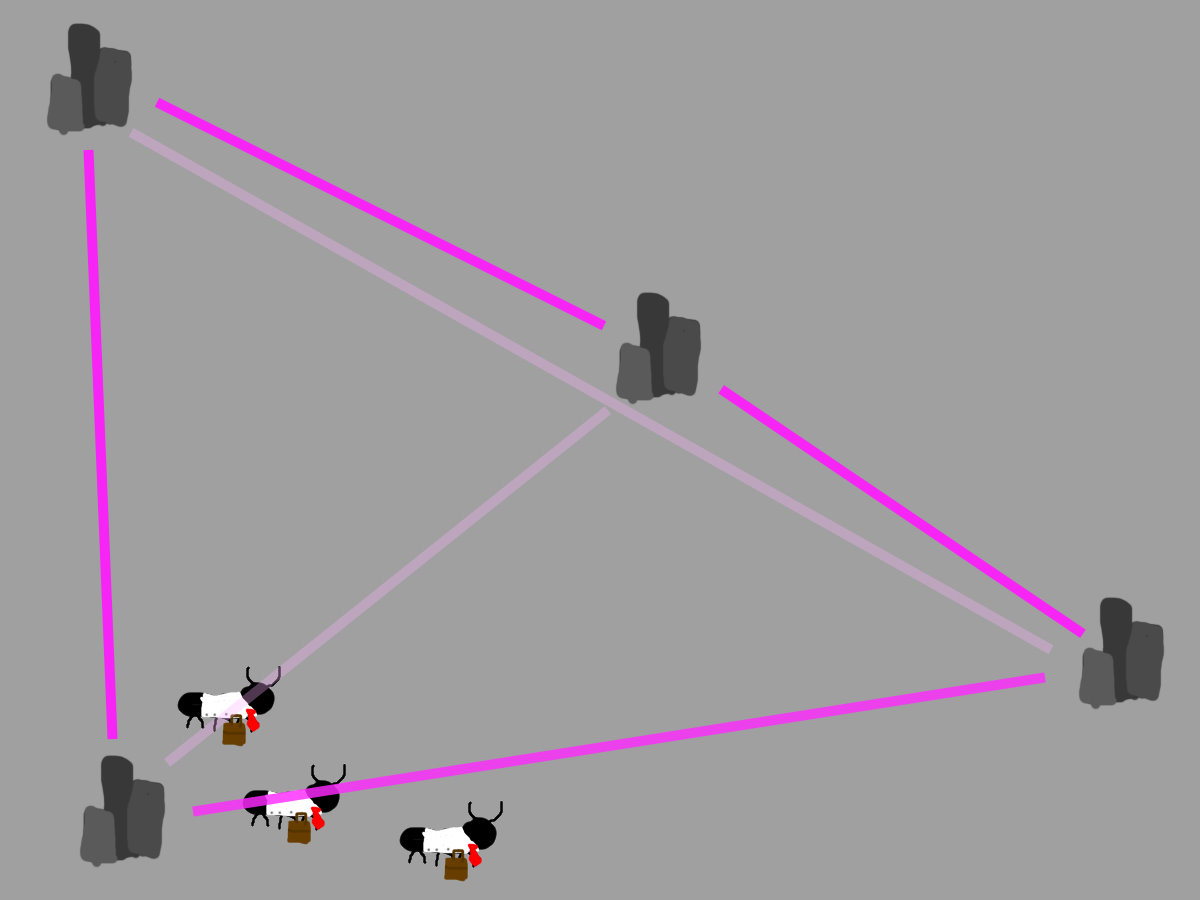
The graph part way through the runs would look like this
The middle path has less pheromones on it because to take that path you would also need to take the longest path
The shortest route is made up of the paths with the most pheromones on them
But how did the ants decide which way to go?
When an ant decides which way to go it follow this probability function
\(P_{xy}\) is the probability that the ant will go from city \(x\) to city \(y\)
\(\tau_{xy}\) is the amount of pheromone to be deposited between city \(x\) to city \(y\)
\(\alpha \geq 0\) is a constant variable to change how strong \(\tau_{xy}\) is
\(\eta_{xy}\) is the attractiveness of a route,
in a tsp is the inverse of the distance from city \(x\) to city \(y\)
Can be represented as \(\frac{1}{d_{xy}}\) where \(d\) is the distance from city \(x\) to city \(y\)
Note
This is information is not known to normal ants, however these ants are business ants and are each given a GPS when they are hired
the sum \(\sum_{z \in \text{allowed}}\) sums the values of other routes from city \(x\)
\(z \in \text{allowed}\) makes sure only cities that have not been visited by this ant are included in the summation
\(\beta\geq1\) is a constant like \(\alpha\) used too change how strong \(\eta_{xy}\) is
\(\tau_{xz}\) and \(\eta_{xz}\) represent the pheromone level and distance of other possible routes from city \(x\)
This Function select_next_city is an implementation of the above formula for ants picking a path
2.3. The Ants Go Marching 1x1
When this is all put together a sequence of ACO goes as followed
First wave of ants travel a complete route randomly
The pheromones are updated based on the first wave of routes
Another wave of ants begin their routes from the first city
The ants probabilistically chose their paths based on the pheromones and distance between the cities
The wave of ants return to the first city and the pheromones are updated based on the paths taken
Repeat steps 3-5 as many times as you want
End the loop
The most efficient route will have been found by our trusty business ants
A basic python implementation of ACO is available on the GitHub