8. \(n\) Queens Genetic Algorithm

  • The purpose of this topic is to emphasize the similarities between genetic algorithm implementations

  • Although the first genetic algorithm implementation was solving a different problem, much of the algorithm is the same

8.1. Problem

  • The optimization version of the \(n\) queens problem is going to be used

    • Given an \(n \times n\) chess board

    • Place \(n\) queens on the chess board

    • While minimizing the number of conflicting/attacking queens

  • In other words, minimize the number of queens in the same row, column, or diagonal

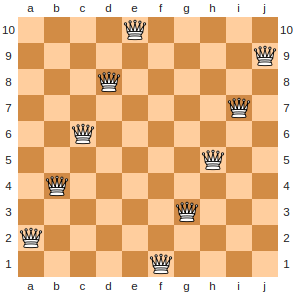
../../_images/10_queens.png

A configuration of \(10\) queens on a \(10 \times 10\) chess board with zero conflicts. This would be an optimal solution where \(n=10\).

  • The reason the optimization version of the problem is being used is because it has a gradient for the search to follow

  • The all or nothing (valid configuration or not) version of the problem has no gradient

  • The phenotype space (problem space) includes all possible configurations of the \(n\) queens on an \(n \times n\) board

    • Assuming queens are not allowed on the same square, this is \(n \times n \choose n\)

  • However, as previously discussed, by using a permutation encoding, the genotype space (search space) is only \(n!\)

8.2. Initialization

  • Before evolution can begin, an initial population of candidate solutions

8.2.1. Representation

  • The permutation representation previously discussed will be used

    • A chromosome will be a list of length \(n\)

    • Each of the \(n\) indices correspond to each of the \(n\) queens

    • Each index will be the queen’s respective column in the chess board

    • The elements within the list will be a permutation of the integers between \(0\) and \(n-1\)

    • The value at each index will be the queen’s respective row in the chess board

  • Since the values and indices are unique, no two queens can be in the same row or column

  • An example chromosome when \(n=8\) is

    <0, 5, 7, 6, 3, 2, 1, 4>

8.2.2. Population

  • A population is a list of chromosomes

    [<0, 5, 7, 6, 3, 2, 1, 4>,
 <4, 5, 2, 3, 6, 7, 1, 0>,
 <0, 1, 2, 3, 4, 5, 6, 7>,
 ...
 ...
 <4, 3, 2, 7, 6, 1, 0, 5>]

  • The chromosomes, and thus the population, will be randomly generated for this implementation of a genetic algorithm

48    population = []
49    population_fitness = []
50    for _ in range(POPULATION_SIZE):
51        chromosome = sample(range(N_QUEENS), k=N_QUEENS)
52        population.append(chromosome)

  • The number of chromosomes within the population is defined by a hyperparameter called POPULATION_SIZE

  • The length of the chromosomes will match the number of queens, which is defined by the hyperparameter N_QUEENS

  • The chromosomes are permutations of the sequence of integers from \(0\) to \(n-1\)

  • Note that sample is from Python’s random library

8.3. Evaluation

  • The fitness function will count the number of conflicting queens

  • Each pair of conflicting queens will only be counted once

  • With the representation used, it’s not possible for two queens to be in the same row or column

  • Thus, only the diagonals need to be checked

23def attacking_fitness(chromosome: list) -> int:
24    """
25    Count the number of attacking queens in the provided queen placements. To count each attacking pair only once, the
26    check for attacking only happens in the forward direction (from index 0 towards n). With the permutation
27    representation, attacking can only happen in a diagonal, thus the check for attacking is to check only +/- offset,
28    where offset is the number of indices away the queens are from each other. For example, consider the chromosome
29    [?, ?, 4, 3, 6, 1, ?, ?]. The queen at index 2 is attacking 3 queens: it attacks the queen at index 3 as it is
30    offset 1 and 4-1=3, it is attacking the queen at index 4 as it is offset 2 and 4+2=6, and it is attacking the queen
31    at index 5 as it is offset 3 and 4-3=1.
32
33    :param chromosome: Chromosome (queen placements) to evaluate
34    :return: The number of attacking queens.
35    """
36    total_attackers = 0
37    for attacker_column, attacker_row in enumerate(chromosome):
38        for victim_index in range(attacker_column + 1, len(chromosome)):
39            offset = victim_index - attacker_column
40            victim_row = chromosome[victim_index]
41            if (attacker_row - offset) == victim_row or (attacker_row + offset) == victim_row:
42                total_attackers += 1
43    return total_attackers

  • For each queen, check the up and down diagonals to the right

    • There is no need to check to the left as any conflict to the left would already be counted

  • The basic idea here is

    • Given a queen at index attacker_column with value attacker_row

    • In order for a queen offset indices away with the value victim_row to be in the same diagonal

    • The value of victim_row must be equal to attacker_row - offset or attacker_row + offset

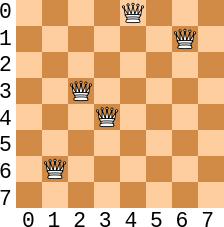
../../_images/8_queens_conflicts.png

\(8 \times 8\) chess board configuration with 4 conflicts. Only \(5\) queens are shown here for demonstration purposes.

  • Consider the above figure and the chromosome <?, 6, 3, 4, 0, ?, 1, ?>

    • The question marks represent irrelevant values for this example

  • When evaluating the queens from left to right

    • The queen at index 1 has a value of 6 and conflicts with two queens

      • It conflicts with the queen at index 3

        • The offset is 2 and the value at index 1 equals the value at index 3 minus the offset 2

        • 6 - 2 == 4

      • It also conflicts with the queen at index 6

        • The offset is 5 and the value at index 6 equals the value at index 6 minus the offset 5

        • 6 - 5 == 1

    • The queen at index 2 also has a conflict with the queen at index 3

      • The offset is 1 and the value at index 2 equals the vlaue at index 3 plus the offset 1

      • 3 + 1 == 4

    • Lastly, the queen at index 3 conflicts with the queen at index 6

      • 4  - 3 == 1

    • As mentioned above, there is no need to look to the left of any queen as those conflicts would already be counted

      • For example, the queen at index 6s conflicts were already counted

  • With this fitness function, the fitness of each candidate solution within the population can be calculated and stored

58        population_fitness = []
59        for chromosome in population:
60            fitness = attacking_fitness(chromosome)
61            population_fitness.append(fitness)

8.4. Selection

  • Tournament selection will be used here

    • It’s simple, and effective

65        mating_pool = []
66        for _ in range(POPULATION_SIZE):
67            tournament_indices = choices(range(POPULATION_SIZE), k=TOURNAMENT_SIZE)
68            chromosome = tournament_selection(population, population_fitness, tournament_indices, direction=-1)
69            mating_pool.append(chromosome)

  • Mind the use of the argument direction

    • This indicates that chromosomes with lower fitness values are better

    • By default it assumes higher fitness is better

23def tournament_selection(
24    population: list, population_fitness: list, selected_indices: list[int], direction: int = 1
25) -> list:
26    """
27    Select the chromosome with the maximum/minimum fitness value of the chromosomes in the tournament. The chromosomes
28    in the tournament if its index is contained within the selected_indices list. By default, the function selects for
29    maximum fitness.
30
31    :param population: Population of chromosomes to select from
32    :param population_fitness: Fitness values of the population
33    :param selected_indices: List of indices in the tournament
34    :param direction: +1 for maximizing fitness, -1 for minimizing fitness
35    :return: A copy of the selected chromosome
36    :raises ValueError: If the list of selected indices is empty or contains an out-of-bounds index
37    """
38    if len(selected_indices) == 0:
39        raise ValueError(f"List of indices in the tournament must be non empty: {selected_indices}")
40    for index in selected_indices:
41        if index < 0 or index > len(population_fitness) - 1:
42            raise ValueError(f"List of indices in the tournament contains out-of-bounds index: {index}")
43    max_value = population_fitness[selected_indices[0]] * direction
44    max_index = selected_indices[0]
45    for index in selected_indices:
46        if population_fitness[index] * direction > max_value:
47            max_value = population_fitness[index] * direction
48            max_index = index
49    return population[max_index][:]

8.5. Variation Operators

  • Given the permutation representation, special considerations should be made when implementing the variation operators

  • The operators should ensure the chromosome remain a permutation

    • Consider a one point crossover on permutations

           v                    v
[0, 1, 2, 3, 4]      [0, 1, 2, 1, 0]
                 ->
[4, 3, 2, 1, 0]      [4, 3, 2, 3, 4]
       ^                    ^

    • This crossover may destroy the fact that the chromosomes are permutations

8.5.1. Crossover

  • An order crossover is commonly used for permutation representations

  • Keep all elements between two randomly selected indices

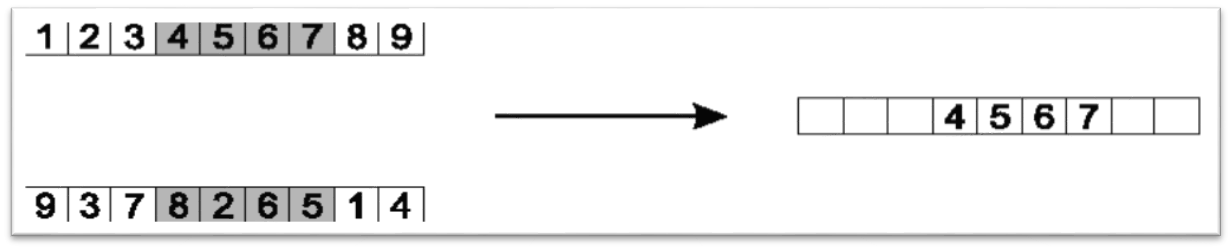
../../_images/order_crossover_copy.png

Keep the segment of the chromosome between two arbitrarily selected indices. This only shows one of the two children that this crossover would produce.

  • Then, copy the elements from chromosome \(A\), in order, if they do not appear in chromosome \(B\)

    • Start copying from after the kept segment

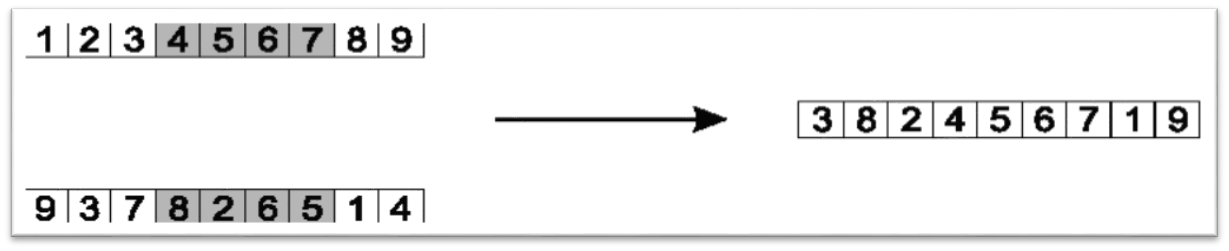
../../_images/order_crossover_remaining.png

Copy the elements from the other parent, in order, starting after the kept segment. Only copy values that are not already contained within the child. Again, this only shows one of the two children this crossover would produce.

 1def order_crossover(parent_1: list, parent_2: list, start_index: int, end_index: int) -> tuple[list, list]:
 2    """
 3    Order crossover. All elements between the two indices are moved to the children and the remaining missing elements
 4    are copied in the order that they appear in the other parent. Copying starts at end_index and returns to index zero
 5    when the end of the chromosome is hit. For example, indices of 2 and 5, [0,1,2,3,4,5,6], [4,6,3,5,2,0,1] ->
 6    [?,?,2,3,4,?,?], [?,?,3,5,2,?,?] -> [6,5,2,3,4,0,1], [1,4,3,5,2,6,0]. Out of order indices, indices with a
 7    difference of 0, and indices covering the whole length of the chromosome are allowed, but result in no change.
 8
 9    :param parent_1: Chromosome to be used in crossover
10    :param parent_2: Chromosome to be used in crossover
11    :param start_index: Starting index of copied segment
12    :param end_index: Ending index of copied segment (excluded in segment)
13    :return: The two chromosomes after the crossover is applied
14    :raises ValueError: If the parents are not the same length of if an index is out-of-bounds
15    """
16
17    def copy_missing_elements(parent: list, child: list, start_index: int, end_index: int) -> list:
18        """
19        Copy the missing elements from the other parent into the child. Elements are copied in order that they appear
20        in the parent, starting at the end index, and looping to index 0 where necessary.
21
22        :param parent: Chromosome to copy missing elements from
23        :param child: Chromosome to have missing elements copied too
24        :param start_index: Starting index of copied segment (where to stop copying missing elements to)
25        :param end_index: Ending index of copied segment (where to start copying missing elements from)
26        :return: child chromosome with the missing elements copied
27        """
28        source_index = end_index % len(parent_1)
29        target_index = end_index % len(parent_1)
30        while target_index != start_index:
31            if parent[source_index] not in child[start_index:end_index]:
32                child[target_index] = parent[source_index]
33                target_index = (target_index + 1) % len(parent_1)
34            source_index = (source_index + 1) % len(parent_1)
35        return child
36
37    if len(parent_1) != len(parent_2):
38        raise ValueError(f"chromosomes must be the same length: {len(parent_1)}, {len(parent_2)}")
39    if start_index < 0 or end_index < 0 or start_index > len(parent_1) - 1 or end_index > len(parent_1):
40        raise ValueError(f"Index out-of-bounds: {start_index}, {end_index}")
41    child_1 = parent_1[:]
42    child_2 = parent_2[:]
43    if start_index > end_index:
44        return child_1, child_2
45    child_1 = copy_missing_elements(parent_2, child_1, start_index, end_index)
46    child_2 = copy_missing_elements(parent_1, child_2, start_index, end_index)
47    return child_1, child_2

8.5.2. Mutation

  • Similar to crossover, one must be careful with the choice of mutation when working with permutations

  • Fortunately, swap mutation is a very simple mutation that is permutation safe

    • Select two indices and swap the values between them

../../_images/swap_mutation.png

Swap mutation on some chromosome. The values at indices 1 and 4 are swapped in this example.

38def swap_mutation(parent: list, index_1: int, index_2: int) -> list:
39    """
40    Swap mutation. Swap the values between the two specified indices. For example, with swap indices of 0 and 3,
41    [0, 1, 2, 3, 4] -> [3, 1, 2, 0, 4]. Providing the same index for both index values results in no change.
42
43    :param parent: Chromosome to be mutated
44    :param index_1: Index to be swapped with index_2
45    :param index_2: Index to be swapped with index_1
46    :return: The chromosome after the mutation is applied
47    :raises ValueError: If either index is out-of-bounds
48    """
49    if index_1 < 0 or index_2 < 0 or index_1 > len(parent) - 1 or index_2 > len(parent) - 1:
50        raise ValueError(f"Index out-of-bounds: {index_1}, {index_2}")
51    child = parent[:]
52    child[index_1], child[index_2] = child[index_2], child[index_1]
53    return child

8.6. Termination Requirement

  • A generational GA will be used with a pre set number of generations defined by the hyperparameter GENERATIONS

56    for generation in range(GENERATIONS):
57        # [begin-evaluation]
58        population_fitness = []
59        for chromosome in population:
60            fitness = attacking_fitness(chromosome)
61            population_fitness.append(fitness)
62        # [end-evaluation]
63
64        # [begin-selection]
65        mating_pool = []
66        for _ in range(POPULATION_SIZE):
67            tournament_indices = choices(range(POPULATION_SIZE), k=TOURNAMENT_SIZE)
68            chromosome = tournament_selection(population, population_fitness, tournament_indices, direction=-1)
69            mating_pool.append(chromosome)
70        # [end-selection]
71
72        # [begin-crossover]
73        for i in range(0, POPULATION_SIZE, 2):
74            if random() < CROSSOVER_RATE:
75                index_one = randrange(N_QUEENS)
76                index_two = randrange(N_QUEENS)
77                start_index = min(index_one, index_two)
78                end_index = max(index_one, index_two)
79                chromosome_1, chromosome_2 = order_crossover(mating_pool[i], mating_pool[i + 1], start_index, end_index)
80                mating_pool[i] = chromosome_1
81                mating_pool[i + 1] = chromosome_2
82        # [end-crossover]
83
84        # [begin-mutation]
85        for i in range(POPULATION_SIZE):
86            if random() < MUTATION_RATE:
87                index_one = randrange(N_QUEENS)
88                index_two = randrange(N_QUEENS)
89                chromosome = swap_mutation(mating_pool[i], index_one, index_two)
90                mating_pool[i] = chromosome
91        # [end-mutation]
92
93        population = mating_pool

  • This loop performs

    • Evaluation

    • Selection

    • Crossover

    • Mutation

  • Once the loop runs to completion, some final results are calculated and reported

    • Calculate the final populations fitness

    • Report the population and the population’s fitness

 97    population_fitness = []
 98    for chromosome in population:
 99        fitness = attacking_fitness(chromosome)
100        population_fitness.append(fitness)
101    print(population_fitness)
102    print(population)

8.7. For Next Class