3. Boolean Logic
Much of the following will likely be a review of already well understood concepts
This content is covered for completeness, but will be kept at a relatively high level
3.1. Boolean Operators and Operands
Boolean logic is a form of algebra that operates on boolean values that can take on only two states
These states are typically called true and false
Depending on context, these are sometimes referred to as On/Off,
1/0, or high voltage/low voltage
Within the algebra, the operands are values that take on one of these two states
The operators act on these operands to produce a new boolean value
Note
If this terminology is throwing you off, remember that this is like the integer operators/operands you are familiar with. Consider the expression \(1 + 2\). The operands here are integers \(1\) and \(2\) and the operator is \(+\), which means addition. Here, addition is an operator that takes two integer values and produces a new integer value.
There are three basic boolean operators
\(not\)
Unary operator — only operates on a single operand to produce a single value
Given some boolean value \(a\), invert it
In other words, if \(a\) is true, not \(a\) is false, and vice versa
Typically denoted as \(\lnot a\) or sometimes \(\overline a\)
\(and\)
Binary operator — operates on two operands to produce a single value
Given boolean values \(a\) and \(b\), return true if both values are true, false otherwise
Denoted as \(a \land b\)
\(or\)
Binary operator — operates on two operands to produce a single value
Given boolean values \(a\) and \(b\), return true if both or either are true, false otherwise
Denoted as \(a \lor b\)
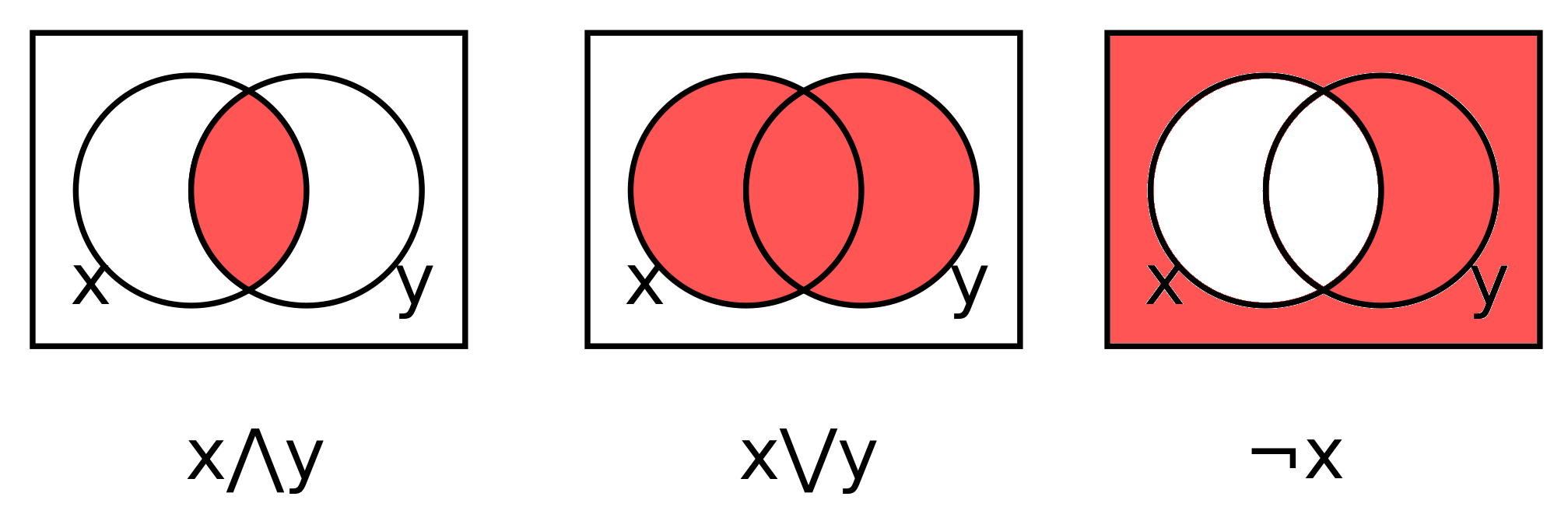
Visual representations of the basic boolean operators with Venn diagrams. The images represent \(and\), \(or\), and \(not\) respectively.
There are additional boolean operators that can be made up from the three basic operators
Three of these are commonly used within the context of computer architecture, thus they will be presented here
\(Exclusive\) \(or\) (\(xor\))
Binary operator — operates on two operands to produce a single value
Given boolean values \(a\) and \(b\), return true if either are true, false otherwise
Similar to \(or\), but if both are true, it returns false
Denoted as \(a \oplus b\)
Equivalent to \((a \lor b) \land \lnot (a \land b)\)
\(not\) \(or\) (\(nor\))
Literally \(not\) \(or\)
Sometimes denoted as \(\overline \lor\)
Equivalent to \(\lnot (a \lor b)\)
Functionally complete — can be used to generate all other boolean operators
\(not\) \(and\) (\(nand\))
Literally \(not\) \(and\)
Sometimes denoted as \(\overline \land\)
Equivalent to \(\lnot (a \land b)\)
Functionally complete — can be used to generate all other boolean operators
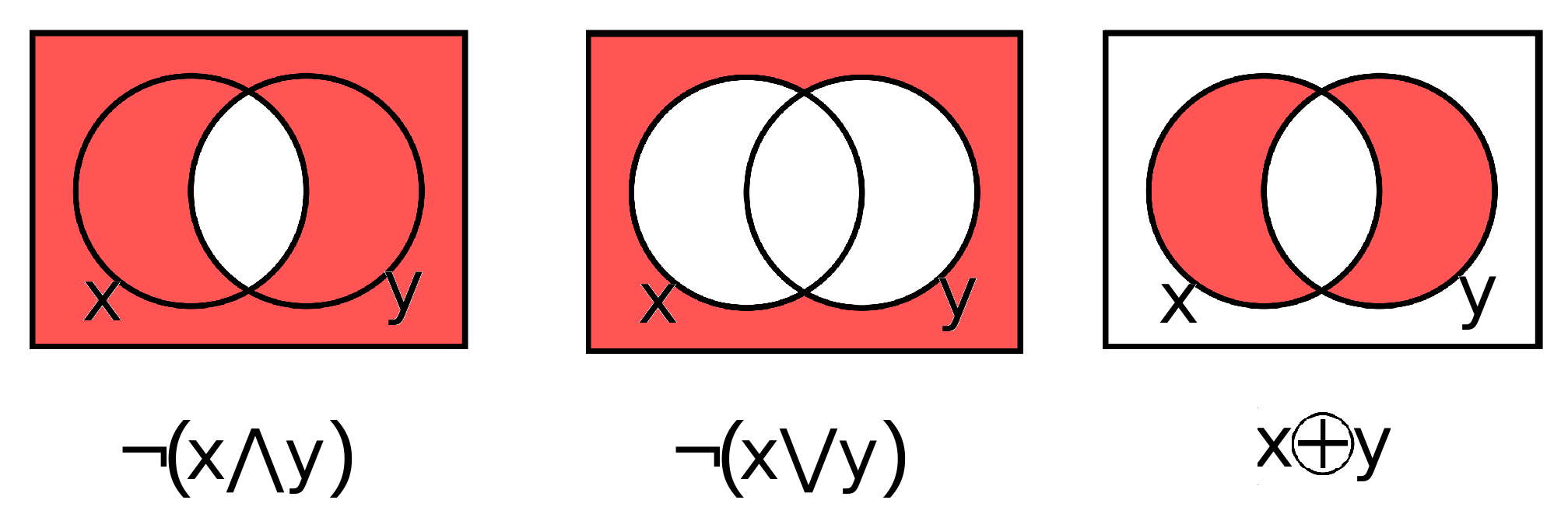
Visual representations of the additional boolean operators with Venn diagrams. The images represent \(nand\), \(nor\), and \(xor\) respectively.
3.2. Truth Tables
Truth tables provide a structured visualization of all possible truth values for logical expressions
These are probably best understood with examples
Below is a truth table for the above boolean operators for all possible combinations of values for two operands
\(a\) |
\(b\) |
\(\lnot a\) |
\(a \land b\) |
\(a \lor b\) |
\(a \oplus b\) |
\(\lnot (a \land b)\) |
\(\lnot (a \lor b)\) |
||
|---|---|---|---|---|---|---|---|---|---|
\(false\) |
\(false\) |
\(true\) |
\(false\) |
\(false\) |
\(false\) |
\(true\) |
\(true\) |
||
\(false\) |
\(true\) |
\(true\) |
\(false\) |
\(true\) |
\(true\) |
\(true\) |
\(false\) |
||
\(true\) |
\(false\) |
\(false\) |
\(false\) |
\(true\) |
\(true\) |
\(true\) |
\(false\) |
||
\(true\) |
\(true\) |
\(false\) |
\(true\) |
\(true\) |
\(false\) |
\(false\) |
\(false\) |
In the context of digital circuits, it is common to use
0and1in place of \(false\) and \(true\)Going forward,
0and1will be used for this course
Note
The empty columns do not have any formal meaning. They are included here for visual clarity.
3.2.1. Building Out the Truth Table
Notice the \(\lnot (a \land b)\) and \(\lnot (a \lor b)\) columns in the truth tables are compound operations
They are made up of two operations — \(not\) and \(and\)/\(or\)
These columns are the inverse of the basic and/or columns in the table
Literally \(not\) the result of those columns
Consider a more complex compound expression — \((a \land \lnot b) \lor \lnot c\)
It is often helpful to break the operation down into parts that are easier to calculate
Then, build out a truth table to solve each part individually
\(a\) |
\(b\) |
\(c\) |
\(\lnot b\) |
\(\lnot c\) |
\(a \land \lnot b\) |
\((a \land \lnot b) \lor \lnot c\) |
|||
|---|---|---|---|---|---|---|---|---|---|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
Activity
Create and complete a truth table for the boolean expression \(\lnot(a \land b) \lor (a \land \lnot b)\).
\(a\) |
\(b\) |
\(\lnot b\) |
\(a \land b\) |
\(a \land \lnot b\) |
\(\lnot(a \land b)\) |
\(\lnot(a \land b) \lor (a \land \lnot b)\) |
|||
|---|---|---|---|---|---|---|---|---|---|
3.3. Properties of Logical Operators
There are several algebraic properties that hold for boolean logic
Most of these are intuitive, but will be presented here for completeness
Identity for \(\lor\) |
\(a \lor false = a\) |
Identity for \(\land\) |
\(a \land true = a\) |
Idempotence for \(\lor\) |
\(a \lor a = a\) |
Idempotence for \(\land\) |
\(a \land a = a\) |
Annihilator for \(\lor\) |
\(a \lor true = true\) |
Annihilator for \(\land\) |
\(a \land false = false\) |
Associativity of \(\lor\) |
\(a \lor (b \lor c) = (a \lor b) \lor c\) |
Associativity of \(\land\) |
\(a \land (b \land c) = (a \land b) \land c\) |
Commutativity of \(\lor\) |
\(a \lor b = b \lor a\) |
Commutativity of \(\land\) |
\(a \land b = b \land a\) |
Complementation 1 |
\(a \land \lnot a = false\) |
Complementation 2 |
\(a \lor \lnot a = true\) |
Double negation |
\(\lnot (\lnot a) = a\) |
Distributivity of \(\lor\) over \(\land\) |
\(a \lor (b \land c) = (a \lor b) \land (a \lor c)\) |
Distributivity of \(\land\) over \(\lor\) |
\(a \land (b \lor c) = (a \land b) \lor (a \land c)\) |
Absorption 1 |
\(a \lor (a \land b) = a\) |
Absorption 2 |
\(a \land (a \lor b) = a\) |
De Morgan’s 1 |
\(\lnot a \lor \lnot b = \lnot (a \land b)\) |
De Morgan’s 2 |
\(\lnot a \land \lnot b = \lnot (a \lor b)\) |
Note
If the absorption laws are unclear, consider the corresponding distributive and idempotent laws. For example, below is the first absorption law:
\(a \lor (a \land b) = (a \lor a) \land (a \lor b) = a \land (a \lor b)\)
If \(a\) is \(false\), given the \(\land\) annihilator law, the expression evaluates to \(false\).
\(false \land (false \lor b) = false\)
If \(a\) is \(true\), given the \(\land\) identity law, the expression evaluates to the result of \((a \lor b)\), which, given the \(\lor\) annihilator law, evaluates to \(true\), therefore, the whole expression evaluates to \(true\).
\(true \land (true \lor b) = true \land true = true\)
If still not convinced, below is the truth table for the first absorption law.
\(a\) |
\(b\) |
\(a \land b\) |
\(a \lor (a \land b)\) |
||
|---|---|---|---|---|---|
|
|
|
|
||
|
|
|
|
||
|
|
|
|
||
|
|
|
|
The proof follows similar for the second annihilation law.
3.3.1. De Morgan’s Law
Warning
Although consistently numbered here, the labels of the first and second De Morgan’s laws is arbitrary.
De Morgan’s laws are of particular interest in the context of computer architecture
Given the popularity of \(nor\) and \(nand\) in circuit design
De Morgan’s laws are as follows
\(\lnot a \lor \lnot b = \lnot(a \land b)\)
\(\lnot a \land \lnot b = \lnot(a \lor b)\)
Consider that the right hand side of both equations are \(nand\) and \(nor\) respectively
This means that, not only can \(nand\) be made with \(not\) and \(and\), but also with \(not\) and \(or\)
One does not even need the \(and\) operator to create \(nand\)
In fact, given only \(not\) and \(or\), one can create \(and\)
\(\lnot(\lnot a \lor \lnot b) = \lnot(\lnot(a \land b)) = a \land b\)
This would work the same for \(nor\) being made with \(not\) and \(and\)
The below truth table provides an exhaustive proof of De Morgan’s laws
\(a\) |
\(b\) |
\(\lnot a\) |
\(\lnot b\) |
\(a \lor b\) |
\(a \land b\) |
\(\lnot a \lor \lnot b\) |
\(\lnot a \land \lnot b\) |
\(\lnot (a \lor b)\) |
\(\lnot (a \land b)\) |
|---|---|---|---|---|---|---|---|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
De Morgan’s laws may not be immediately obvious, but think about what they mean
Visualizations may help with grasping the intuition
Consider the first law
\(\lnot a \lor \lnot b = \lnot(a \land b)\)
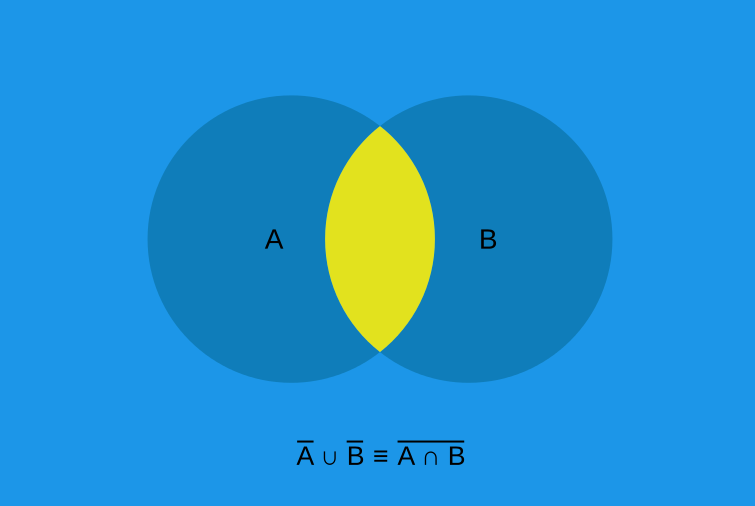
Visualization of De Morgan’s first law. In this figure, blue is what is included in the result, yellow is what is excluded. Here, \(\cup\) (set union) is equivalent to or (\(\lor\)) and the \(\cap\) (set intersect) is equivalent to and (\(\land\)).
It is easier to see how the above figure represents \(\lnot(a \land b)\)
Think of the Venn diagram of \(and\), then invert it
But also imagine what \(\lnot a\) and \(\lnot b\) would be
\(\lnot a\) would be everything but what is within \(a\), including that which is in \(b\)
\(\lnot b\) would be everything but what is within \(b\), including that which is in \(a\)
It may be helpful to think of two versions of the figure, one which is \(\lnot a\) and the other \(\lnot b\)
Then, \(or\) would be the union of these two images, which is the same as the above figure
Union being, keep all points from both images
Now consider the second law
\(\lnot a \lor \lnot b = \lnot(a \land b)\)
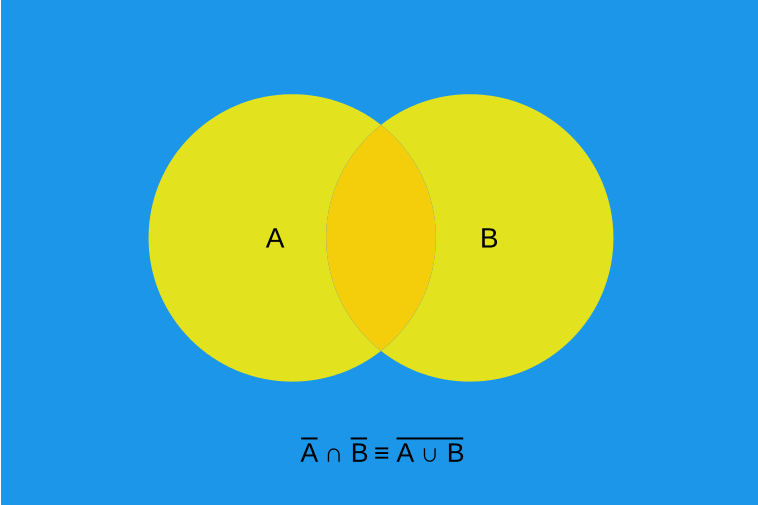
Visualization of De Morgan’s second law. In this figure, blue is what is included in the result, yellow is what is excluded. Here, \(\cup\) (set union) is equivalent to or (\(\lor\)) and the \(\cap\) (set intersect) is equivalent to and (\(\land\)).
Similar to the first law, it is easier to see how the above figure represents \(\lnot(a \lor b)\)
Imagine what \(\lnot a\) and \(\lnot b\) would be
It’s easier to think of two versions of the image, one for each \(\lnot a\) and \(\lnot b\)
Then, \(and\) would be the intersect of these two images, which is the same as the above figure
Intersect being, only keep the points that exist in both images
3.4. For Next Time
Read Chapter 3 Sections 1
3 pages