12. Two’s Complement

• As long as enough bits are available, any positive integer (and zero) can be represented

  • With \(n\) bits, the numbers \(0\) through \(2^{n} - 1\) can be represented

  • This would be an unsigned integer

• However, how can negative numbers be represented?

12.1. Sign Bit

• All binary numbers so far have been unsigned

  • They have only represented positive integers or zero

• Consider the following table with the number \(5\) represented as an eight bit binary number

\(128\)	\(64\)	\(32\)	\(16\)	\(8\)	\(4\)	\(2\)	\(1\)
0	0	0	0	0	1	0	1

• To determine what number this represents, add the place value of each bit that is 1

• In the above example, the bits representing the value \(4\) and \(1\) are 1, thus the number is \(5\)

  • \(4 + 1 = 5\)

• As discussed in an earlier topic, this works the same way with base ten numbers

• Addition in binary also works the same as base ten, but with only two symbols

  • Add up the values in each position, and carry to the next significant position if needed

Carry			1	1						\(1\)
Number 1	0	1	0	1	1	1	0	0			\(9\)	\(2\)
Number 2	1	0	0	1	1	0	1	0		\(1\)	\(5\)	\(4\)
Sum	1	1	1	1	0	1	1	0		\(2\)	\(4\)	\(6\)

• The above table shows addition of two numbers, in binary and decimal

  • The left side is binary addition, the right side is decimal

• A simple way to represent negative numbers is to use the most significant bit as a sign bit

• Consider the number \(5\) — 00000101

• To represent \(-5\), replace the most significant bit (left most) with a 1 — 10000101

  • With this strategy, 10000101 would be \(-5\), not \(133\)

• Since the most significant bit is used as a sign, fewer positive numbers can be represented

  • But negative numbers are now possible

• Below is a table showing all the possible values a four bit binary number can represent with the use of a sign bit

All four bit values representable with the use of a sign bit

1111	\(-7\)
1110	\(-6\)
1101	\(-5\)
1100	\(-4\)
1011	\(-3\)
1010	\(-2\)
1001	\(-1\)
1000	\(-0\)
0000	\(0\)
0001	\(1\)
0010	\(2\)
0011	\(3\)
0100	\(4\)
0101	\(5\)
0110	\(6\)
0111	\(7\)

12.1.1. Problems and Limitations

• One may have started to notice some issues with this strategy

• First, there are two patterns that represent the number \(0\)

  • 1000 meaning \(-0\)

  • 0000 meaning \(0\)

  • Although one is negative, this does not have any meaning for integers

• Another issue is that the pattern for the numbers change depending on the number of bits

• With positive numbers, this is not a problem

  • 0101 is the same as 00000101

  • They both represent \(5\)

• But consider the four bit binary number 1101 and the eight bit number 10000101

  • Both represent the number \(-5\), yet they have different patterns

• And finally, another issue is addition

• With decimal numbers, adding a negative number is the same as subtraction

  • \(5 + -5 = 0\)

• If one were to try to add a negative number with a sign bit, it will not work properly

Adding a negative binary number with a sign bit

Carry	1	1		1
Number 1		0	1	0	1		\(5\)
Number 2		1	1	0	1		\(-5\)
Sum	1	0	0	1	0		\(2?\)

• Even if one ignores the fact that the sign bit got carried to a fifth bit, the arithmetic does not work out

12.2. One’s Compliment

• A potential alternative to using a sign bit is ones complement

• The strategy is similar to a sign bit, but with ones complement, all bits are flipped for negative numbers

  • Take the complement of each bit

All four bit values representable with the one’s complement

1000	\(-7\)
1001	\(-6\)
1010	\(-5\)
1011	\(-4\)
1100	\(-3\)
1101	\(-2\)
1110	\(-1\)
1111	\(-0\)
0000	\(0\)
0001	\(1\)
0010	\(2\)
0011	\(3\)
0100	\(4\)
0101	\(5\)
0110	\(6\)
0111	\(7\)

• Like with a sign bit, it is simple to identify negative numbers by looking for a 1 in the most significant bit

• But the issue of the pattern for negative numbers changing depending on the number of bits is somewhat resolved

• Consider the number \(-3\)

  • With three bits, \(-3\) is represented as 100

  • With four bits, \(-3\) is represented as 1100

• Although the pattern is different, the idea is that negative numbers have an infinite number of leading 1s

  • As opposed to an infinite number of 0s as with positive numbers

12.2.1. Problems and Limitations

• Unfortunately, ones complement still has the oddity of having two patterns for the number \(0\)

  • 0000 for \(0\)

  • 1111 for \(-0\)

• Further, addition with negative numbers is still not perfect

Adding a negative binary number with one’s complement

Carry
Number 1		0	1	0	1		\(5\)
Number 2		1	0	1	0		\(-5\)
Sum		1	1	1	1		\(-0\)

• The above example results in a correct addition, but issues arise with non zero results

Note

With binary addition and a fixed number of bits, any carry that results in an overflow will ultimately be ignored. For example, consider the four bit addition of 1111 (\(7\)) + 0001 (\(1\)). The result is clearly 10000 (\(8\)), but since there are only four bits available, the overflowed value is lost, and the result would be 0000.

Adding a negative binary number with one’s complement

Carry	1	1
Number 1		0	1	0	1		\(5\)
Number 2		1	1	0	0		\(-3\)
Sum	(ignore overflow) 1	0	0	0	1		\(1?\)

Adding a negative binary number with one’s complement

Carry	1	1
Number 1		1	1	0	1		\(-2\)
Number 2		0	1	1	0		\(6\)
Sum	(ignore overflow) 1	0	0	1	1		\(3?\)

Adding a negative binary number with one’s complement

Carry	1	1	1	1
Number 1		1	0	1	1		\(-4\)
Number 2		1	1	0	1		\(-2\)
Sum	(ignore overflow) 1	1	0	0	0		\(-7?\)

• The fact that the overflow value is lost is important for addition of negative numbers to work

• However, when looking at these results, it is clear that addition with negative numbers doesn’t quite work

• Except for when the sum is \(0\), all results are one less than what they should be

• In fact, considering \(-0\) is a strange number, maybe the sum should be \(0\), which is also off by one

  • Refer to the table of four bit ones complement binary numbers to make this more clear

  • Notice how each sum is one row above where the sum should be

12.3. Two’s Compliment

• With one’s complement, the issue with arithmetic and negative numbers could be resolved by adding one to the result

• However, due to the associative property, one could be added before any arithemetic

• In other words, to create negative numbers, one could flip all bits and add one

• This idea is called two’s complement

All four bit values representable with the two’s complement

1000	\(-8\)
1001	\(-7\)
1010	\(-6\)
1011	\(-5\)
1100	\(-4\)
1101	\(-3\)
1110	\(-2\)
1111	\(-1\)
0000	\(0\)
0001	\(1\)
0010	\(2\)
0011	\(3\)
0100	\(4\)
0101	\(5\)
0110	\(6\)
0111	\(7\)

• Notice that with this encoding of negative numbers, the peculiarity of having two zeros is eliminated

• Further, like with one’s complement, different bit length numbers don’t have different patterns for negative numbers

  • Remember, imagine that negative numbers have an infinite number of leading 1s

• And finally, arithmetic with negative numbers works perfectly

Adding a negative binary number with two’s complement

Carry	1	1	1	1
Number 1		0	1	0	1		\(5\)
Number 2		1	0	1	1		\(-5\)
Sum	(ignore overflow) 1	0	0	0	0		\(0\)

Adding a negative binary number with two’s complement

Carry	1	1		1
Number 1		0	1	0	1		\(5\)
Number 2		1	1	0	1		\(-3\)
Sum	(ignore overflow) 1	0	0	1	0		\(2\)

Adding a negative binary number with two’s complement

Carry	1	1	1
Number 1		1	1	1	0		\(-2\)
Number 2		0	1	1	0		\(6\)
Sum	(ignore overflow) 1	0	1	0	0		\(4\)

Adding a negative binary number with two’s complement

Carry	1	1
Number 1		1	1	0	0		\(-4\)
Number 2		1	1	1	0		\(-2\)
Sum	(ignore overflow) 1	1	0	1	0		\(-6\)

• With two’s complement, notice how there is an uneven number of positive and negative numbers

  • With four bits, there are seven positive numbers and eight negative numbers

• With a single encoding for zero, there will be a mismatch between the number of positive and negative numbers

• However, with four bits, there are still a total of 16 unique values that can be represented with four bits

12.4. Negation and Subtraction

• There are many ways one could physically implement two’s complement negation

• A simple strategy is to literally NOT every bit and add one via a full adder

Negating an eight bit binary value to two’s complement encoding. Here, the value is negated by applying NOT to each bit and adding one.

• In the above example, the input bits are flipped with a NOT gate and one is added with a full adder

  • Here, the full adder is adding zero to the inverted input value with a carry in bit that is always 1

• Subtraction can be done by providing a way to negate one of the input values to a full adder

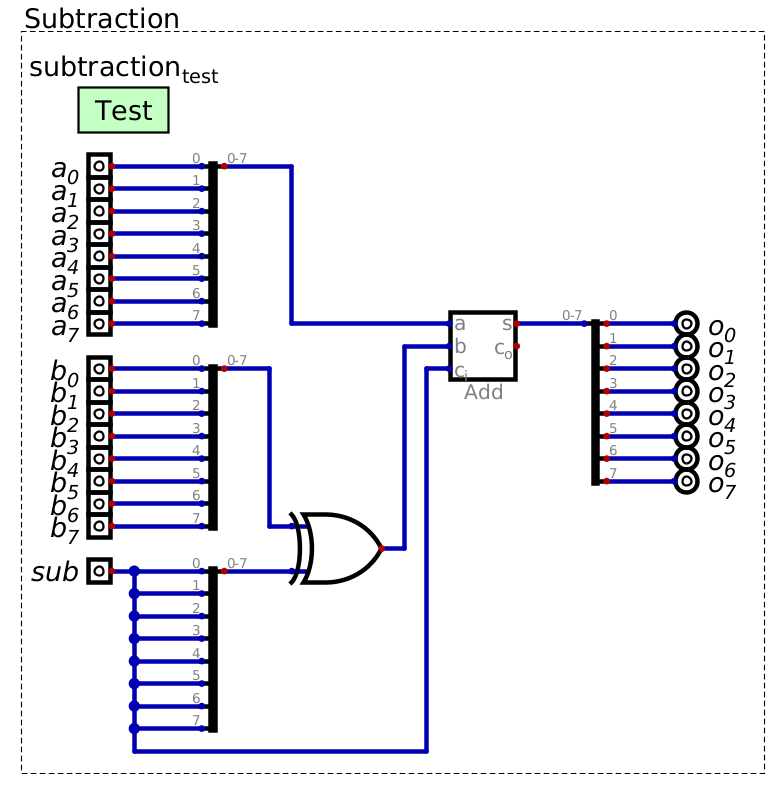
A full adder with the ability to perform subtraction. Here, \(sub\) controls whether the adder is performing subtraction as it provides a way to flip the bits of one of the inputs with the use of XOR while also controlling the value on the adder’s carry in (\(C_{i}\)).

• Here, a \(sub\) input provides a way to toggle the negation of one of the inputs

  • When \(sub\) is high, XOR will flip the bits of the input and the carry in input to the adder will be high

  • When \(sub\) is low, XOR has no affect and the carry in value for the adder will be low

• With this configuration, the full adder can be toggled to perform addition or subtraction

12.5. For Next Time

• Something?